Exercises

Evaluate the integral I₍₀₎ = +∞ ∫ 0 e^{−γ r^k} dr.
Evaluate the integral I_(n) = +∞ ∫ 0 rⁿ e^{−γ r^k} dr.
Evaluate the normalization constant of a Slater-type orbital (STO) and a Gaussian-type orbital (GTO) in spherical coordinates.
Evaluate the normalization constant of a Gaussian-type orbital (GTO) in Cartesian coordinates.
Evaluate the normalization constant of a Slater-type orbital (STO) in Cartesian coordinates.
Use the variation method to show that the orbital energies obtained by solving the Schrödinger equation for hydrogenic atoms with the Slater-type orbital χ_n,ℓ,m(ζ; r,θ,φ) = R_n(ζ; r) Y_ℓ,m(θ,φ) as a trial function are an upper bound to the exact orbital energies, E_n = − Z² / 2 n² . Compare the behavior of Slater-type orbitals against that of exact hydrogenic orbitals, and find the relationship between hydrogenic and Slater-type orbitals.
Find the average distance of the electron from the nucleus in each state of the hydrogen atom.
Compare the most probable distances of the electron from the proton in the hydrogen 1s, 2s and 2p states with the corresponding average radius.

Exercise 1: Evaluate the integral I₍₀₎ = +∞ ∫ 0 e^{−γ r^k} dr and discuss the two cases of k = 1 (e.g., 1s Slater-type orbital) and k = 2 (e.g., 1s Gaussian-type orbital).

By using the method of u-substitution, [N5] let u = γ r^k so that r = ( u / γ )^{^{^¹⁄_k}} and dr = (γ)^−¹⁄_k (u)^{(¹⁄_k)−1} / k du. Now substitute into the integrand, replacing all forms of r:

I₍₀₎ = (γ)^−¹⁄_k k −∞ ∫ 0 (u)^{(¹⁄_k)−1} e^−u du = (γ)^−¹⁄_k k Γ ( 1 k ) = (γ)^−¹⁄_k Γ (1 + 1 k )

(E1.1)

The improper integral in eq. (E1.1) is easily recognized as an Euler integral of the second kind[L1Euler integrals. Encyclopedia of Mathematics.], i.e. the gamma function Γ(¹⁄_k).[L2Wikipedia contributors, "Gamma function," Wikipedia, The Free Encyclopedia., L3Weisstein, Eric W. "Gamma Function." From MathWorld--A Wolfram Web Resource.]

Case k = 1: 1s-STO. For positive integers n, the gamma function is related to the factorial function: Γ(n) = (n − 1)!, so that for k = 1 the gamma function is Γ(2) = 1! = 1 and I₍₀₎ = 1 / γ . The same result can be obtained by direct integration, after u-substitution (i.e. u = − γ r, from which r = − ^u⁄_γ and dr = − ¹⁄_γ du):

I₍₀₎ = +∞ ∫ 0 e^{−γ r} dr
I₍₀₎ = − 1 γ −∞ ∫ 0 e^u du
I₍₀₎ = − 1 γ [e^u ]^{^{^−∞}}₀
I₍₀₎ = − 1 γ ( lim u → −∞ e^u − e⁰ )
I₍₀₎ = 1 γ

(E1.2)

Case k = 2: 1s-GTO. The gamma function evaluated at k = 2 is [L2Wikipedia contributors, "Gamma function," Wikipedia, The Free Encyclopedia., L3Weisstein, Eric W. "Gamma Function." From MathWorld--A Wolfram Web Resource.] Γ ( 1 / 2 ) = √π and I₍₀₎ = 1 / 2 √ π / γ . The value of Γ(z) at z = ¹⁄₂ can be evaluated using Euler's reflection formula [L4Weisstein, Eric W. "Reflection Relation." From MathWorld − A Wolfram Web Resource.]

Γ(z) Γ(1 − z) = π sin (π z)

(E1.3)

The result can be proven by direct integration, after u-substitution (i.e. u² = γ r², from which r = √ 1 / γ u and dr = √ 1 / γ du):

I₍₀₎ = +∞ ∫ 0 e^−r² dr = √ 1 γ +∞ ∫ 0 e^−u² du

(E1.4)

To derive the value for I₍₀₎, the following steps are used. First, the value of I₍₀₎ is squared. Second, the squared value is rewritten as a double integral. Third, the double integral is evaluated by transforming to polar coordinates. Fourth, the I₍₀₎ is explicitly solved for. The first two steps yield

I₍₀₎² = 1 γ +∞ ∫ 0 e^−x² dx × +∞ ∫ 0 e^−y² dy
I₍₀₎² = 1 γ +∞ ∫ 0 +∞ ∫ 0 e^{−(x² + y²)} dx dy

(E1.5)

where it has been taken into account that the integration variable u is silent, in the sense that it can be chosen freely and, if necessary, replaced with a symbol more appropriate to the context. The region which defines the first quadrant, is the region of integration for the integral in eq. (E1.5). The bivariate transformation x = r cos θ, y = r sin θ will transform the integral problem from cartesian coordinates, (x, y), to polar coordinates, (r, θ). These new variables will range from 0 ≤ r ≤ ∞ and 0 ≤ θ ≤ ^π⁄₂ for the first quadrant. The Jacobian determinant of the transformation is

det |J| = det

^∂x⁄_∂r	^∂x⁄_∂θ
^∂y⁄_∂r	^∂y⁄_∂θ

= det

cos θ	−r sin θ
sin θ	r cos θ

= r cos²θ + r sin²θ = r

(E1.6)

so that the area elements is

dx dy = r dr dθ

(E1.7)

Hence, eq. (E1.5) can be written as

I₍₀₎² = 1 γ +∞ ∫ 0 +∞ ∫ 0 e^{−(x² + y²)} dx dy = 1 γ π/2 ∫ 0 +∞ ∫ 0 e^−r² r dr dθ
I₍₀₎² = − 1 2 γ π/2 ∫ 0 dθ −∞ ∫ 0 e^u du
I₍₀₎² = − 1 2 γ [θ ]^{^{^π/2}}₀ ⋅ [e^u ]^{^{^−∞}}₀ = − 1 2 γ ( π 2 − 0 ) ( lim u → −∞ e^u − e⁰ ) = − π 4 γ ( 0 − 1 )
I₍₀₎² = π 4 γ

(E1.8)

where the substitution u = −r², du = −2rdr, and dr = − 1 / 2 r du has been applied to solve the radial integral. Hence,

I₍₀₎ = 1 2 √ π γ

(E1.9)

as it was anticipated.

Solution. The solution of this exercise is summarized by the following equation

I₍₀₎ = +∞ ∫ 0 e^{−γ r^k} dr = (γ)^−¹⁄_k Γ (1 + 1 k ) = { 1 γ for k = 1 (STO), 1 2 √ π γ for k = 2 (GTO),

(E1.10)

Exercise 2: Evaluate the integral I_(n) = +∞ ∫ 0 rⁿ e^{−γ r^k} dr and discuss the two cases of k = 1 (e.g., Slater-type orbital) and k = 2 (e.g., Gaussian-type orbital).

Start from the solution of Exercise 1, which gives the result for n = 0. Then use the Leibniz integral rule (which establishes that a derivative and an integral can be interchanged, allowing differentiation under the integral sign):[L5 Weisstein, Eric W. "Leibniz Integral Rule." From MathWorld − A Wolfram Web Resource.]

∂ⁿ ∂γⁿ +∞ ∫ 0 e^{−γ r^k} dr = +∞ ∫ 0 ∂ⁿ ∂γⁿ e^{−γ r^k} dr (k = 1, 2)

(E2.1)

The n-th derivative of I₍₀₎ in eq. (E1.10) equals the product of the gamma function Γ (1 + 1 / k ) times the n-th derivative of (γ)^−¹⁄_k with respect to γ:

I_{(n) =

∂ⁿ
I₍₀₎
/

∂γⁿ

I_(n)²
= (−1)ⁿ

1
/

k

(1 +

1
/

k

)

(2 +

1
/

k

) …

(n − 1 +

1
/

k

)
(γ)^{−¹⁄_k−n}
Γ

(1 +

1
/

k

)

I_(n)²
= (−1)ⁿ

1⋅(k + 1)⋅(2k +
1)⋅(3k + 1)⋅…⋅[(n−1)
k + 1]
/

kⁿ γ^(nk+1)/k
Γ

(1 +

1
/

k

)

I_(n)²
= (−1)ⁿ

[kn − (k − 1)]!^(k)
/

kⁿ⁺¹ γ^(nk+1)/k
Γ

(

1
/

k

)

I_(n)²
= (−1)ⁿ

1
/

k γ^(nk+1)/k
Γ

(n +

1
/

k

)}

(E2.2)

where n!^(k) denotes the k-th multifactorial of n [L6Weisstein, Eric W. "Multifactorial." From MathWorld--A Wolfram Web Resource.] and some general properties of the gamma function have been used.[L7Wikipedia contributors, "Particular values of the gamma function," Wikipedia, The Free Encyclopedia.]

On the other hand, the n-th derivative of the integrand in eq. (E1.10) with respect to γ is

∂ⁿ ∂γⁿ e^{−γ r^k} = (−1)ⁿ r^nk e^{−γ r^k}

(E2.3)

Finally, combining eq (E2.3) and the last equality of eq (E2.2) into eq (E2.1), you get the solution of the exercise:

+∞ ∫ 0 r^nk e^{−γ r^k} dr = 1 k γ^(nk+1)/k Γ (n + 1 k )

(E2.4)

which can be specified for k = 1 (STO):

+∞ ∫ 0 rⁿ e^{−γ r} dr = 1 γⁿ⁺¹ Γ(n + 1) = n! γⁿ⁺¹

(E2.5)

and for k = 2 (GTO):

+∞ ∫ 0 r²ⁿ e^{−γ r²} dr = 1 2 γ^(2n+1)/2 Γ (n + 1 2 ) = (2n − 1)!! 2ⁿ⁺¹ √ π γ²ⁿ⁺¹

(E2.6)

Setting ½n → n in eq (E2.6) you get

+∞ ∫ 0 rⁿ e^{−γ r²} dr = 1 2 γ^(n+1)/2 Γ ( n + 1 2 ) = (n − 1)!! √ π 2(2γ)ⁿ⁺¹

(E2.7)

In the eqs (E2.5-7) the identities Γ(n + 1) = n!, Γ (n + 1 / 2 ) = (2n − 1)!! / 2ⁿ √π, and Γ ( n + 1 / 2 ) = (n − 1)!! / 2^n/2 √π have been used.

Exercise 3: Evaluate the normalization constant of a Slater-type orbital (STO, k = 1) and a Gaussian-type orbital (GTO, k = 2), expressed in spherical coordinates χ_n,ℓ,m(η,k; r,θ,φ) = R_n(η,k; r) Y_ℓ,m(θ,φ), where the Y_ℓ,m(θ,φ) are orthonormalized spherical harmonics, and R_n(η,k; r) = N_n(η,k) rⁿ⁻¹ e^{−η r^k} is the radial function, with N_n(η,k) being the normalization constant to be determined.

The normalization constant of an atomic orbital χ(r) can be computed by imposing the condition

∫ ℝ³ |χ(r)|² d³r = 1

(E3.1)

which, for STOs and GTOs in spherical coordinates, can be written as

(E3.2)

and, since π ∫ 0 2π ∫ 0 |Y_ℓ,m(θ,φ)|² sinθ dθ dφ = 1 by definition, what remains is

+∞ ∫ 0 r² |R_n(η,k; r)|² dr = N_n(η,k)² +∞ ∫ 0 r²ⁿ e^{−2η r^k} dr = 1

(E3.3)

From the last identity of the previous equation, you get

N_n(γ,k) = [ +∞ ∫ 0 r²ⁿ e^{−γ r^k} dr ]^{^{^−¹⁄₂}}

(E3.4)

where γ = 2η. The values of the integral in eq (E3.4) for k = 1 and k = 2 are given by eqs (E2.5) and (E2.6), respectively. Hence

N_n(γ,k) = { √ γ²ⁿ⁺¹ (2n)! for k = 1 (STO), √ 2ⁿ⁺¹ (2n − 1)!! ( γ²ⁿ⁺¹ π )^{^{^¹⁄₄}} for k = 2 (GTO),

(E3.5)

(cf equations (5) and (10) in reference [1Gomes, A. S. P.; Custodio, R.
J. Comput. Chem. 2002, 23, 1007-1012.]).

Exercise 4: Evaluate the normalization constant N_a,b,c(α) of a Gaussian-type orbital (GTO) expressed in cartesian coordinates χ_a,b,c(α; x,y,z) = N_a,b,c(α) x^a y^b z^c e^−αr², where a, b, and c are integers, whose sum equals the azimuthal quantum number ℓ = a + b + c.

The normalization constant of an atomic orbital χ(r) is computed by imposing the condition

∫ ℝ³ | χ_a,b,c(α; x,y,z) |² d³r = 1

(E4.1)

Substituting χ(r) with its expression in Cartesian coordinates and observing that r² = x² + y² + z², the previous equation can be rearranged as follows:

+∞ ∫ −∞ +∞ ∫ −∞ +∞ ∫ −∞ | N_a,b,c(α) x^a y^b z^c e^{−α (x² +y² +
z²)} |² dx dy dz =
= [ N_a,b,c(α) ]² +∞ ∫ −∞x^2a e^{−2α x²} dx +∞ ∫ −∞y^2b e^{−2α y²} dy +∞ ∫ −∞z^2c e^{−2α z²} dz =
= [ N_a,b,c(α) ]² I_x I_y I_z = 1

(E4.2)

According to eq (E2.6), the integral I_x is given by

I_x = +∞ ∫ −∞x^2a e^{−2α x²} dx = 2 +∞ ∫ 0x^2a e^{−2α x²} dx = (2a − 1)!! 2^a √ π (2α)^2a+1

(E4.3)

Similar expressions hold for the integrals I_y and I_z, so that eq (E4.2) can be rewritten as

[ N_a,b,c(α) ]² I_x I_y I_z = [ N_a,b,c(α) ]² (2a − 1)!! (2b − 1)!! (2c − 1)!! 2^a+b+c √ π³ (2α)^2(a+b+c)+3 = 1

(E4.4)

Hence (cf equation (12) in reference [1Gomes, A. S. P.; Custodio, R.
J. Comput. Chem. 2002, 23, 1007-1012.]):

N_a,b,c(α) = √ 2^a+b+c (2a − 1)!! (2b − 1)!! (2c − 1)!! ( (2α)^2(a+b+c)+3 π³ )^{^{^¹⁄₄}}
N_a,b,c(α) = √ 2^{2(a+b+c)+³⁄₂} (2a − 1)!! (2b − 1)!! (2c − 1)!! α^{a+b+c+³⁄₂} π^³⁄₂

(E4.5)

Exercise 5: Evaluate the normalization constant N_a,b,c,k(ζ) of a Slater-type orbital (STO) expressed in cartesian coordinates χ_a,b,c,k(ζ; x,y,z) = N_a,b,c,k(ζ) x^a y^b z^c r^k−1 e^{−ζ r}, where a, b, and c are integers, whose sum equals the azimuthal quantum number ℓ = a + b + c, and k is the difference between the principal quantum number n and the azimuthal quantum number ℓ, k = n − ℓ = n − (a + b + c).

The solution (cf equation (7) in reference [1Gomes, A. S. P.; Custodio, R.
J. Comput. Chem. 2002, 23, 1007-1012.]) is

N_a,b,c,k(ζ) = √ (2ζ)^2k+1 (2k)! (2a + 2b + 2c + 1)!! 4π (2a − 1)!! (2b − 1)!! (2c − 1)!!

(E5.1)

Exercise 6: The time-independent Schrödinger equation (in atomic units) for the hydrogen and hydrogen-like atoms is [2Szabo, A.; Ostlund, N. S.
“Modern Quantum Chemistry - Introduction to Advanced Electronic Structure Theory”
Macmillan Publishing Co., Inc., New York, 1982, p. 33.]

(− 1 2 ∇² − Z r ) ❘χ⟩ = E ❘χ⟩

where Z is the atomic number. Use the variation method with the Slater-type orbital χ_n,ℓ,m(ζ; r,θ,φ) = R_n(ζ; r) Y_ℓ,m(θ,φ) as a trial function to show that the orbital energies are an upper bound to the exact orbital energies (which are given by E_n = − Z² 2 n² ).
Compare the behavior of Slater-type orbitals against that of exact hydrogenic orbitals, and find the relationship between hydrogenic and Slater-type orbitals. Left multiplying both sides of the Schrödinger equation by ⟨χ❘, yields the formal solution

E = ⟨ χ❘ − 1 2 ∇² − Z r ❘χ ⟩ ⟨χ❘χ⟩

(E6.1)

As shown in the statement of the Exercise, the Slater-type function, χ_n,ℓ,m(ζ; r,θ,φ), is the product of the orthonormalized real spherical harmonics, Y_ℓ,m(θ,φ), with the radial function

R_n(ζ; r) = N_n(ζ) rⁿ⁻¹ e^{−ζ r}

(E6.2)

where N_n(ζ) is the normalization constant (cf Exercise 3):

N_n(ζ) = √ (2ζ)²ⁿ⁺¹ (2n)!

(E6.3)

Substituting χ in eq (E6.1) with its explicit expression, yields

E = ⟨ R_n(ζ; r)❘− 1 2 ∇² − Z r ❘R_n(ζ; r) ⟩ ⟨ Y_ℓ,m(θ,φ) ❘ Y_ℓ,m(θ,φ) ⟩ ⟨χ_n,ℓ,m(ζ; r,θ,φ)❘χ_n,ℓ,m(ζ; r,θ,φ)⟩
E = ⟨ R_n(ζ; r)❘− 1 2 ∇² − Z r ❘R_n(ζ; r) ⟩

(E6.4)

In the last equality of eq (E6.4), the normalization conditions of the functions χ_n,ℓ,m(ζ; r,θ,φ), R_n(ζ; r), and Y_ℓ,m(θ,φ) have been taken into account. Substituting the Laplace operator ∇² in eq. (E6.4) with its expression in spherical coordinates yields

E_n = ⟨ R_n(r)❘− 1 2 d² d r² − 1 r d d r − Z r ❘R_n(r) ⟩
E_n = ⟨ R_n(r)❘− ζ² 2 + n ζ − Z r − n (n − 1) 2 r² ❘R_n(r) ⟩
E_n = − ζ² 2 ⟨R_n(r)❘R_n(r)⟩ + (n ζ − Z) ⟨R_n(r)❘r⁻¹❘R_n(r)⟩ − n (n − 1) 2 ⟨R_n(r)❘r⁻²❘R_n(r)⟩

(E6.5)

where

⟨R_n(r)❘R_n(r)⟩ = 1

(E6.6)

⟨R_n(r)❘r⁻¹❘R_n(r)⟩ = (2ζ)²ⁿ⁺¹ (2n)! +∞ ∫ 0 r²ⁿ⁻¹ e^{−2ζ r} dr = (2ζ)²ⁿ⁺¹ (2n)! ⋅ (2 n − 1)! (2 ζ)²ⁿ = ζ n

(E6.7)

⟨R_n(r)❘r⁻²❘R_n(r)⟩ = (2ζ)²ⁿ⁺¹ (2n)! +∞ ∫ 0 r²ⁿ⁻² e^{−2ζ r} dr = (2ζ)²ⁿ⁺¹ (2n)! ⋅ (2 n − 2)! (2 ζ)²ⁿ⁻¹ = 2 ζ² n (2n − 1)

(E6.8)

so that eq (E6.5) becomes

E_n = − ζ² 2 + ζ (n ζ − Z) n − (n − 1) ζ² 2n − 1
E_n = ζ [n ζ − 2 (2n − 1) Z] 2 n (2n − 1)

(E6.9)

Differentiating eq (E6.9) with respect to ζ and equating to zero yields

d E_n d ζ = n ζ − (2n − 1) Z n (2n − 1) = 0 ⇒ ζ = 2n − 1 n Z

(E6.10)

so that the orbital energy has the expression

E_n = − Z² 2 n² (2n − 1)

(E6.11)

which overestimates the exact value by a factor of (2n − 1) and only in the case of n = 1 gives the exact ground state energy, which is -0.5 hartree for the hydrogen atom (Z = 1).

Exact hydrogenic wavefunctions and Slater-type orbitals. The exact solution of the time-independent Schrödinger equation for hydrogenic atoms is described in many quantum-mechanical text-books (e.g. [5Leonard I. Schiff
“Quantum Mechanics”
McGraw-Hill, 1968, Chapter 16, pp. 88-99., 6Paul A. Tipler and Gene Mosca
“Physics for Scientists and Engineers: Extended Version”.
W. H. Freeman, 2003, Section 36-4, p. 1181., 7David A. B. Miller
“Quantum Mechanics for Scientists and Engineers”
Cambridge University Press, 2008, Chapter 10, pp. 259-278.]) as well as on the web (e.g. [L9?Rudi Winter
“Solving Schrödinger's equation for the hydrogen atom”
Online resource.]) and is not reported here. We simply mention that the eigenfunctions can be factored as follows

ψ_n,ℓ,m(α; r,θ,φ) = R_n,ℓ(α; r) Y_ℓ,m(θ,φ)

(E6.12)

where Y_ℓ,m(θ,φ) are orthonormalized real spherical harmonics and the R_n,ℓ(α; r) are the eigenfunctions of the one-dimensional Schrödinger equation for the radial distance r:

R_n,ℓ(α; r) = N_n,ℓ(α) (2αr)^ℓ L^2ℓ+1_n−ℓ−1(2αr) e^−αr

(E6.13)

where α is the ratio between the atomic number Z and the principal quantum number n, α = Z n , and N_n,ℓ(α) is the normalization constant,

N_n,ℓ(α) = √ (n − ℓ − 1)! 2n (n + ℓ)! (2 α)³

(E6.14)

The functions L^2ℓ+1_n−ℓ−1(2αr) are the associated Laguerre polynomials which, in the notation of Abramowitz and Stegun,[8Milton Abramowitz and Irene A. Stegun, eds.
“Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables”.
New York: Dover, 1972, § 22.3, p. 775.] are defined as

L^2ℓ+1_n−ℓ−1(2αr) = n − ℓ − 1 ∑ q=0 (−1)^q ( n + ℓ n − ℓ − q − 1 ) 1 q! (2αr)^q
L^2ℓ+1_n−ℓ−1(2αr) = n − ℓ − 1 ∑ q=0 (−1)^q (n + ℓ)! (n − ℓ − q − 1)! (q + 2ℓ + 1)! q! (2αr)^q

(E6.15)

It's worth noting that the overall “size” of the hydrogenic wavefunctions becomes larger with larger n. The number of zeros in the wavefunction is n − 1. The associated Laguerre polynomials in the radial wavefunction have n − ℓ − 1 zeros, and the spherical harmonics have ℓ nodal “circles”. For every value of the principal quantum number n there is a degeneracy equal to n², i.e. there are n² different atomic orbitals, all of which possess the same value for the energy, E_n. These degenerate orbitals are characterized by the n possible values of the azimuthal quantum number ℓ (ℓ = 0, 1, …, n−1) and, for every value of ℓ, by the (2ℓ + 1) possible values of the magnetic quantum number m (m = −ℓ, …, −2, −1, 0, 1, 2, …, ℓ). The main difference between hydrogenic wavefunctions and Slater-type orbitals is the presence of nodes in the former. Unlike hydrogenic atomic orbitals, whose radial function depends on both the principal and azimuthal quantum numbers, the radial function of Slater-type orbitals depends only on the principal quantum number. However, it is easy to show that the hydrogenic wavefunction can be written as a linear combination of Slater-type orbitals. In fact, eq (E6.13) can be rewritten as follows

R_n,ℓ(α; r) = N_n,ℓ(α) n − ℓ − 1 ∑ q=0 (−1)^q (n + ℓ)! (n − ℓ − q − 1)! (2ℓ + q + 1)! q! (2αr)^ℓ+q e^−αr

(E6.16)

where you recognize that the product (2αr)^ℓ+q e^−αr is strictly related to the radial part of a Slater orbital by the relationship

(2αr)^ℓ+q e^−αr = (2α)^ℓ+q r^ℓ+q e^−αr = (2α)^ℓ+q R_ℓ+q+1(α; r) N_ℓ+q+1(α)

(E6.17)

which, back-substituted into eq (E6.16), yields

R_n,ℓ(α; r) = n−ℓ−1 ∑ q=0 u_ℓq(n) R_ℓ+q+1(α; r)

(E6.18)

Multiplying both sides of eq (E6.18) by Y_ℓm(θ,φ) yields a similar expression for the full hydrogenic wavefunctions in terms of Slater-type orbitals

ψ_n,ℓ,m(α; r,θ,φ) = n−ℓ−1 ∑ q=0 u_ℓq(n) χ_{ℓ+q+1,ℓ,m}(α; r,θ.φ)

(E6.19)

In both equations (E6.18) and (E6.19) the coefficients u_ℓq(n) are defined as

u_ℓq(n) = (−1)^q (n + ℓ)! (n − ℓ − q − 1)! (2ℓ + q + 1)! q! N_n,ℓ(α) N_ℓ+q+1(α) (2α)^ℓ+q
u_ℓq(n) = (−1)^q [2n (n + ℓ)! (n − ℓ − 1)! (2ℓ + 2q + 2)!]^½ 2n (n − ℓ − q − 1)! (2ℓ + q + 1)! q!

(E6.20)

Explicit expressions of the expansion coefficients u_ℓq(n) are reported in Table E6.1 for the lowest values of n. It's worth noting the special values u_0,0(n) = 1 and u_n−1,0(n) = 1 for every value of n = 1, 2, ….

**Table E6.1** - Expansion coefficients of hydrogenic wavefunctions into Slater-type orbitals.
R_nℓ	R₁	R₂	R₃	R₄	u_ℓq(n),^(a) (q = 0, 1, 2, …, n−ℓ−1)
R₁₀	1				(−1)^q [2 (2q + 2)!]^½ / 2 (− q)! (1 + q)! q! , (q = 0)
R₂₀	1	−√3			(−1)^q [2 (2q + 2)!]^½ / 2 (1 − q)! (1 + q)! q! , (q = 0, 1)
R₂₁		1			(−1)^q [6 (2q + 4)!]^½ / 2 (− q)! (3 + q)! q! , (q = 0)
R₃₀	1	− 2 √3	√10		(−1)^q [2 (2q + 2)!]^½ / (2 − q)! (1 + q)! q! , (q = 0, 1, 2)
R₃₁		2 √6 / 3	−√5		(−1)^q 2 [(2q + 4)!]^½ / (1 − q)! (3 + q)! q! , (q = 0, 1)
R₃₂			1		(−1)^q 2 [5 (2q + 6)!]^½ / (− q)! (5 + q)! q! , (q = 0)
R₄₀	1	− 3 √3	3 √10	−√35	(−1)^q 3 [2 (2q + 2)!]^½ / (3 − q)! (1 + q)! q! , (q = 0, 1, 2, 3)
R₄₁		√5	− 5 √6 / 2	√21	(−1)^q [30 (2q + 4)!]^½ / (2 − q)! (3 + q)! q! , (q = 0, 1, 2)
R₄₂			3 √2 / 2	−√7	(−1)^q 3 [10 (2q + 6)!]^½ / (1 − q)! (5 + q)! q! , (q = 0, 1)
R₄₃				1	(−1)^q 3 [70 (2q + 8)!]^½ / (− q)! (7 + q)! q! , (q = 0)
^(a) Coefficient of R_ℓ+q+1(^Z⁄_n).

For each value of n, the functions u_ℓq(n,α) of Eq (E6.20) define an n×n upper triangular matrix U_n, whose elements U_n,ij (i = ℓ + 1, j = ℓ + q + 1, ℓ = 0, 1, …, n−1, and q = 0, 1, …, n−ℓ−1) are equal to 0 for i > j, and have the expression of eq (E6.20), U_n,ij ≡ U_{n;ℓ+1,ℓ+q+1} = u_ℓq(n,α), for i ≤ j. Therefore, if y_n(α; r) = | R_n,0(α; r), R_n,1(α; r), …, R_n,n−1(α; r) |^† and x_n(α; r) = | R₁(α; r), R₂(α; r), …, R_n(α; r) |^†, eq (E6.18) can be written in matrix notation as y_n(α; r) = U_n x_n(α; r).
Low order (n = 1, …, 5) hydrogen radial wavefunctions are compared in Table E6.2 with the corresponding Slater-type orbitals with three different exponent values (ζ = α, (2n−1)α, Z). For every value of n, the two functions coincide only if ℓ = n − 1 (in addition to sharing the same exponent, α).

**Table E6.2** - Comparison of various low order radial wavefunctions of hydrogenic atoms with the corresponding STO approximations.
R_nℓ	exact hydrogenic orbital R_nℓ(α; r) = √ (n − ℓ − 1)! / 2n (n + ℓ)! (2 α)³ (2αr)^ℓ L^2ℓ+1_n−ℓ−1(2αr) e^−αr α = Z / n	STO approximation R_n(ζ; r) = √ (2ζ)²ⁿ⁺¹ / (2n)! rⁿ⁻¹ e^{−ζ r}
R_nℓ		ζ = Z / n	ζ = (2n − 1) Z / n	ζ = Z
R_1,0 ≡ R_1s	2 √Z³ e^{−Z r}	2 √Z³ e^{−Z r}	2 √Z³ e^{−Z r}	2 √Z³ e^{−Z r}
R_2,0 ≡ R_2s	√2 Z³ / 4 (2 − Z r) e^{−Z r/2}	√6 Z⁵ / 12 r e^{−Z r/2}	9 √2 Z⁵ / 4 r e^{−3Z r/2}	2 √3 Z⁵ / 3 r e^{−Z r}
R_2,1 ≡ R_2p	√6 Z⁵ / 12 r e^{−Z r/2}	√6 Z⁵ / 12 r e^{−Z r/2}	9 √2 Z⁵ / 4 r e^{−3Z r/2}	2 √3 Z⁵ / 3 r e^{−Z r}
R_3,0 ≡ R_3s	2 √3 Z³ / 27 (3 − 2Z r + 2 / 9 Z² r² ) e^{−Z r/3}	2 √30 Z⁷ / 1215 r² e^{−Z r/3}	250 √6 Z⁷ / 243 r² e^{−5Z r/3}	2 √10 Z⁷ / 15 r² e^{−Z r}
R_3,1 ≡ R_3p	√6 Z⁵ / 81 r (4 − 2 / 3 Z r ) e^{−Z r/3}
R_3,2 ≡ R_3d	2 √30 Z⁷ / 1215 r² e^{−Z r/3}
R_4,0 ≡ R_4s	√Z³ / 16 (4 − 3Z r + 1 / 2 Z² r² − 1 / 48 Z³ r³ ) e^{−Z r/4}	√35 Z⁹ / 26880 r³ e^{−Z r/4}	2401 √5 Z⁹ / 3840 r³ e^{−7Z r/4}	2 √35 Z⁹ / 105 r³ e^{−Z r}
R_4,1 ≡ R_4p	√15 Z⁵ / 192 r (4 − Z r + 1 / 20 Z² r² ) e^{−Z r/4}
R_4,2 ≡ R_4d	√5 Z⁷ / 3840 r² (12 − Z r) e^{−Z r/4}
R_4,3 ≡ R_4f	√35 Z⁹ / 26880 r³ e^{−Z r/4}

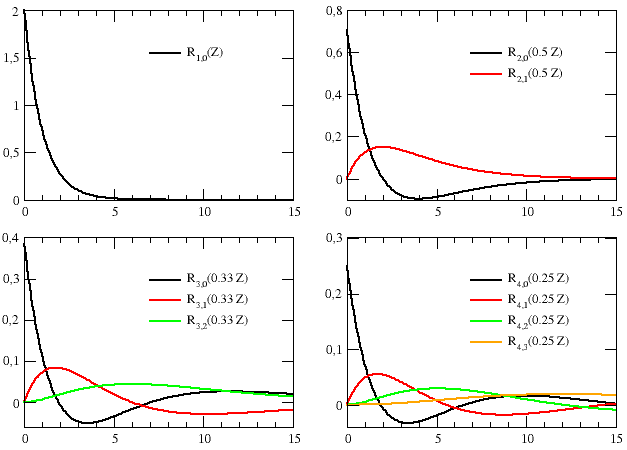
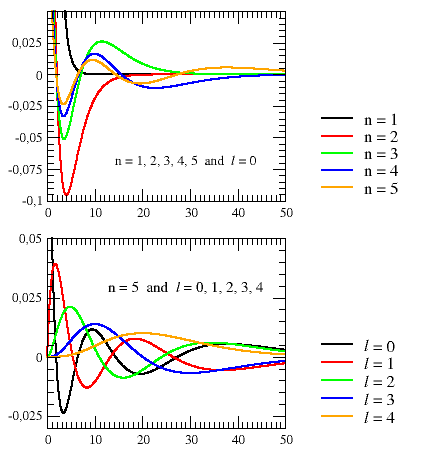
The exercise is completed by the graphs of Figure E6.1, illustrating the behavior of the radial wavefunctions (amplitudes,[N0] R(r)) shown in Table E6.2, and by the graphs of Figures E6.2 and E6.3, which show how the associated squared amplitudes, |R(r)|², and radial densities, ρ(r) = r² |R(r)|², vary as the radius increases.

The radial functions are computed over about 200 points, whose coordinates along a line are expressed in atomic units of length. An ad hoc fortran program provides a human-readable block-data file for each value of n. In each file, the data are structured in (n + 4) columns, the first of which contains the values of the radial coordinate, r. The next n columns contain the values of the hydrogen radial eigenfunctions for ℓ = 0, 1, 2, …, n−1. The last three columns contain the STO values for ζ = Z n , ζ = (2n−1) Z n , and ζ = Z, respectively. C ------------------------------------------------------------------ Program Hydrogen C ------------------------------------------------------------------ C C Compare the radial functions of hydrogenic and Slater-type C orbitals C C ------------------------------------------------------------------ Implicit Double Precision (a-h,o-z) Parameter (nmax=5) Dimension u(nmax), y1(nmax) C-tst Dimension y5(nmax) Data Zero /0.0d0/, One /1.0d0/, Two /2.0d0/ Data RMax /15.0d0/, dr /0.075d0/ C C Table E6.1 C Do n = 1,nmax Write(*,'(/,1x,79("-"),/," Table E6.1 for n = ",i2,/, $ 1x,79("-"))') n Do l = 0,n-1 Call STO_ULK (n,l,u) If (l+1.eq.2) then Write(*,'(10x," l = ",i2,15x,5f12.5)') l,(u(i),i=1,n-l) else if (l+1.eq.3) then Write(*,'(10x," l = ",i2,27x,5f12.5)') l,(u(i),i=1,n-l) else if (l+1.eq.4) then Write(*,'(10x," l = ",i2,39x,5f12.5)') l,(u(i),i=1,n-l) else if (l+1.eq.5) then Write(*,'(10x," l = ",i2,51x,5f12.5)') l,(u(i),i=1,n-l) else Write(*,'(10x," l = ",i2,3x,5f12.5)') l,(u(i),i=1,n-l) end If end Do end Do write(*,*) C C Profiles C iop = 1 Z = one ! atomic number C iu = 10 ju = 20 ku = 30 Do n = 1,nmax iu = iu + 1 ju = ju + 1 ku = ku + 1 write(*,'(" Profiles of Hydrogenic and Slater-type", $ " Orbitals for n =",i2," are written on unit",i3)') n, iu zeta = z/float(n) ! orbital exponent zetamod = zeta * float(2*n-1) C r = - dr do while (r.lt.rmax) r = r + dr C C Hydrogenic Atomic Orbitals Do l = 0, n-1 y1(l+1) = HAO (n,l,z,r,iop) end Do C C Slater-type Orbital, with zeta = Z/n y2 = STO (n,zeta,r,iop) C C Slater-type Orbital, with zeta = Z*(2n-1)/n y3 = STO (n,zetamod,r,iop) C C Slater-type Orbital, with zeta = Z y4 = STO (n,z,r,iop) C C HAO as a linear combination of STOs C (values to be tested against y1) C-tst Do l = 0, n-1 C-tst Call STO_ULK (n,l,u) C-tst y5(l+1) = 0.0d0 C-tst do k=1,n-l C-tst y5(l+1) = y5(l+1) + u(k) * STO(l+k,zeta,r,iop) C-tst end do C-tst end Do C C Write out radial amplitude profiles C write(iu,'(14f12.8)') r, (y1(i),i=1,n), y2, y3, y4 C-tst$ , (y5(i),i=1,n) C C Write out squared radial amplitude profiles C write(ju,'(14f12.8)') r, (y1(i)**2,i=1,n), y2**2, $ y3**2, y4**2 C C Write out radial density profiles C r2 = r*r Do l = 0, n-1 y1(l+1) = r2 * y1(l+1)**2 end Do y2 = r2 * y2**2 y3 = r2 * y3**2 y4 = r2 * y4**2 write(ku,'(14f12.8)') r, (y1(i),i=1,n), y2, y3, y4 C end do end Do End C ------------------------------------------------------------------ Double Precision Function STO (n,z,r,iop) C ------------------------------------------------------------------ C C Return the radial part of a Slater-type orbital C C n ..... principal quantum number (0, 1, 2, ...) C z ..... orbital exponent C r ..... radial distance C iop ... 0 unnormalized C 1 normalized C C ------------------------------------------------------------------ Implicit Double Precision (a-h,o-z) Data One /1.0d0/, Two /2.0d0/ C STO = (r**(n-1)) * exp(-z*r) C C Normalization constant C if (iop.eq.1) then nn = 2*n STO = STO * sqrt( ((Two*z)**(nn+1)) / Fact(nn) ) end If C C Return End C ------------------------------------------------------------------ Double Precision Function HAO (n,l,z,r,iop) C ------------------------------------------------------------------ C C Return the radial part of a hydrogenic atomic orbital C C n ..... principal quantum number (0, 1, 2, ...) C l ..... azimuthal quantum number (0, 1, 2, ..., n-1) C z ..... atomic number C r ..... radial distance C iop ... 0 unnormalized C 1 normalized C C ------------------------------------------------------------------ Implicit Double Precision (a-h,o-z) Data Zero /0.0d0/, One /1.0d0/, Two /2.0d0/ C alpha = z / float(n) ar = alpha*r tar = two*ar s = zero do k = 0, n-l-1 s = s + (tar**(k+l)) * ((-one)**k)/ $ ( fact(n-l-k-1) * fact(l+l+k+1) * fact(k) ) end do HAO = s * fact(n+l) * exp( -ar ) C C Normalization constant C if (iop.eq.1) then CN = ((two*alpha)**3) * fact(n-l-1) / $ ( float(2*n) * fact(n+l) ) HAO = HAO * sqrt( CN ) end If C Return End C ------------------------------------------------------------------ Subroutine STO_ULK (n,l,u) C ------------------------------------------------------------------ C C Return the coefficients required to express the radial part of an C hydrogenic wavefunction as a linear combination of the radial part C of Slater-type orbitals C C n ... principal quantum number (0, 1, 2, ...) C l ... azimuthal quantum number (0, 1, 2, ..., n-1) C z ... orbital exponent C u ... coefficients C C ------------------------------------------------------------------ Implicit Double Precision (a-h,o-z) Data One /1.0d0/, Two /2.0d0/ Dimension u(*) C UA = float(2*n) * fact(n+l) * fact(n-l-1) C j = 0 Do i = 0, n-l-1 j = j + 1 UB = sqrt( UA * fact(2*l + 2*i + 2) ) UD = fact(n-l-i-1) * fact(2*l+i+1) * fact(i) * float(2*n) u(j) = (-One)**i * UB/UD end Do C Return End C ------------------------------------------------------------------ Double Precision Function Fact (N) C ------------------------------------------------------------------ C C The Factorial of a non-negative integer N, denoted by N!, is the C product of all positive integers less than or equal to N. C ------------------------------------------------------------------ Implicit Double Precision (A-H,O-Z) Data One /1.0D0/ C Fact = One If (N.lt.1) return Do I=1,N Fact = Fact * Float(I) end Do C Return End The last step is to use GRACE [LL1"Grace (plotting tool)",
Wikipedia, The Free Encyclopedia, LL2GRACE website] to read the block-data files generated by the fortran code and to arrange the data interactively until the most satisfactory representation is obtained.

**Figure E6.1:** Hydrogen atom radial wavefunctions (amplitudes), *R_n,ℓ*(α; r), from exact solutions of the Schrödinger equation, as a function of the radial distance in units of the Bohr radius. The different graphs refer to increasing values of the principal quantum number n.

**Figure E6.2:** Hydrogen atom radial amplitudes from exact solutions of the Schrödinger equation, *R_n,ℓ*(r), as a function of the radial distance in units of the Bohr radius. Upper: curves are for n = 1, 2, 3, 4, 5 and ℓ = 0. Lower: curves are for n = 5 and ℓ = 0, 1, 2, 3, 4.

The graphs of Figure E6.1 show that each time the quantum number n increases, an additional node is created in the radial wavefunction. This is made more clear in the upper graph of Figure E6.2, which shows the ns radial wavefunctions R_n,s(r) of the hydrogen atom. They differ from the ns orbitals ψ_n,s(r,θ,φ) by a constant angular factor, the spherical harmonic Y₀₀ = 1/√4π. Therefore the ns orbitals are all spherically symmetrical and, like the radial functions, they have n − 1 radial nodes (spherical shells on which the wavefunction equals zero).
Each time the quantum number ℓ is increased (lower graph of Figure E6.2), one of the spherical nodes disappears again. It is replaced by a planar node that goes through the nucleus.
In the ground state of the hydrogen atom, n = 1, the radial wavefunction is nodeless (i.e. all positive). Its maximum is at r = 0, i.e. the point in space with the highest (joint) probability density of finding the electron is actually inside the nucleus! This is true for all the ns orbitals, whose maximum value is at the origin of the radial coordinate. Therefore, only ℓ = 0 electrons have a finite (joint) probability density at the nucleus.

At this point it is appropriate to spend a few words trying to overcome some misunderstanding about the position of the electron in the hydrogen atom. The statement that “the probability density of the electron's position in a ns orbital is maximal at the origin” refers to the Born rule, [LL5Born, M. “The statistical interpretation of quantum mechanics”, Nobel lecture, December 11, 1954.] which postulates that the probability density of finding a particle in some region is proportional to the square of the modulus of the wave function, e.g.

ρ_1s(r,θ,φ) = |ψ_1s(r,θ,φ)|² = |R_1,0(r)|² |Y_0,0(θ,φ)|² = Z³ π e^{−2Z r}

(E6.21)

This is a joint probability density, where the word “joint” stresses the fact that it is linked to the occurrence of a triple of values, one for each of the three variables r, θ, φ. When a joint probability density is multiplied by an infinitesimal volume element (which in polar spherical coordinates is dV = r² sinθ dr dθ dφ) gives the probability that the values of the three variables r, θ, φ fall in that infinitesimal volume element, i.e. the probability of finding the electron there. This probability is infinitesimal, even if the volume element dV is positioned at the origin, where the probability density is maximal. Integrating the probability over a finite volume V yields the electronic charge contained in V and, if V is extended to all space, the total charge that amounts to 1e is retrieved, so satisfying the normalization condition.
Thus, the probability of finding the electron in an infinitesimal volume element can be written as

ρ_n,s(r,θ,φ) r² sinθ dr dθ dφ = |ψ_n,s(r,θ,φ)|² r² sinθ dr dθ dφ

(E6.22)

The use of spherical-polar coordinates is convenient because people are used to think of an atom as some sort of fuzzy ball of electrons around a small, central, heavy nucleus, and extend such a mental picture even to bonded atoms in molecules and crystals. In this case, the ns orbitals of the hydrogen atom are spherically-symmetrical (i.e. do not depend on θ and φ), so that integration of eq. (E6.22) over θ and φ gives 4π, the total solid angle of a sphere:

ρ_n,s(r) dr = |ψ_n,s(r)|² r² dr π ∫ 0 sinθ dθ 2π ∫ 0 dφ = 4π |ψ_n,s(r)|² r² dr

(E6.23)

Eq. (E6.23) introduces a “marginal” probability density, namely the “radial” probability density:

ρ_n,s(r) = 4π |ψ_n,s(r)|² r² = 4π |R_n,0(r)|² |Y_0,0|² r² = |R_n,0(r)|² r²

(E6.24)

Eq. (E6.24) can be generalized for all the permissible values of the quantum numbers n and ℓ, thanks to the form of the wave functions (ψ_n,ℓ,m or χ_n,ℓ,m) that are defined as the product of the orthonormalized real spherical harmonics, Y_ℓ,m(θ,φ), with a radial function, R_n,ℓ(α; r) or R_n(ζ; r):

(E6.25)

where the double integral expresses the normalization condition of the real spherical harmonics and is equal to one.

Rather than considering the probability of finding the electron in one particular small element of space, the radial density is associated to the probability of finding the electron in a spherical shell of space of infinitesimal thickness, 4π r² dr (cf eq. E6.23).[N4Volume of a spherical shell of infinitesimal thickness] The plot of radial probability passes through zero at r = 0 since the surface area, 4π r², the surface area of a sphere of zero radius is zero. As the radius of the sphere is increased, the surface area of the spherical shells increases. However, it increases more rapidly with increasing r than the joint electron probability density decreases, so that the radial probability has a maximum at r_max = a₀, which is the Bohr radius for the n = 1 orbit (cf first graph in Figure E6.3). Thus more of the electronic charge is present at a distance a₀, out from the nucleus than at any other value of r.

Where is the electron in a hydrogen atom? http://spiff.rit.edu/classes/phys314/lectures/hyd_probs/hyd_probs.html Most probable point for finding an electron in the 1s orbital of a Hydrogen atom https://chemistry.stackexchange.com/questions/84726/most-probable-point-for-finding-an-electron-in-the-1s-orbital-of-a-hydrogen-atom http://www.falstad.com/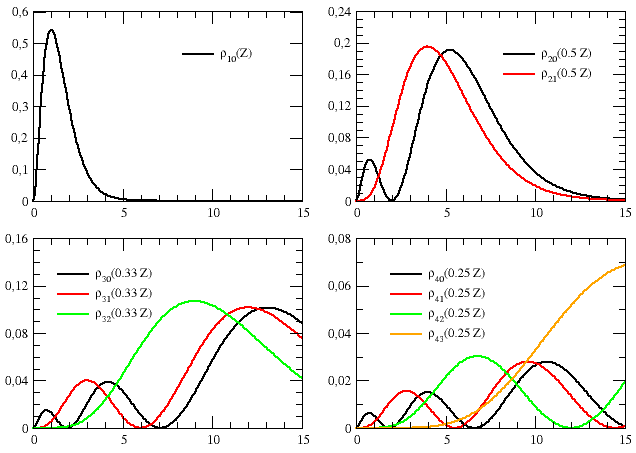

**Figure E6.3:** Hydrogen atom radial densities, *ρ_n,ℓ*(α; r) = r² [*R_n,ℓ*(α; r)]², from exact solutions of the Schrödinger equation, as a function of the radial distance in units of the Bohr radius. The different graphs refer to increasing values of the principal quantum number n.

**Figure E6.4:** Hydrogen atom radial wavefunctions, *R_n*(ζ; r) (left graph), and radial densities, *ρ_n*(ζ; r) = r² [*R_n*(ζ; r)]² (right graph), from approximated solutions of the Schrödinger equation based on Slater-type orbitals with exponent ζ = Z, as a function of the radial distance r in units of the Bohr radius.

Exercise 7: find the average distance of the electron from the nucleus in each state of the hydrogen atom. The average distance of the electron from the nucleus is found by weighting each possible distance with the probability that the electron will be found at that distance

<r>_n.ℓ = +∞ ∫ 0 r ρ_n,ℓ(r) dr

(E7.1)

where ρ_n,ℓ(r) = r² |R_n,ℓ(r)|² is the radial probability density. Eq. (E7.1) can be easily generalized to compute the m-th moment of the radial distribution

<r^m>_n.ℓ = +∞ ∫ 0 r^m ρ_n,ℓ(r) dr

(E7.2)

Using eqs. (E6.13) and (E6.14), eq. (E7.2) becomes

<r^m>_n.ℓ = +∞ ∫ 0 r^m+2 |R_n,ℓ(r)|² dr = (n − ℓ − 1)! 2n (n + ℓ)! (2 α)³ +∞ ∫ 0 r^m+2 (2αr)^2ℓ [L^2ℓ+1_n−ℓ−1(2αr)]² e^−2αr dr

(E7.3)

Introducing the scaled distance s = 2αr, from which r^m+2 = s^m+2 (2α)^m+2 and dr = ds 2α, and rewritting the associated Laguerre polynomials L^2ℓ+1_n−ℓ−1(2αr) of eq. (E6.15) as

L^2ℓ+1_n−ℓ−1(s) = n−ℓ ∑ q=1 (−s)^q−1 t_q

(E7.4)

where

t_q = (n + ℓ)! [ (n − ℓ − q)! (q + 2ℓ)! (q − 1)! ]⁻¹ (q = 1, 2, 3, …, n−ℓ)

(E7.5)

yields

<r^m>_n.ℓ = n^m−1 (n − ℓ − 1)! (n + ℓ)! 2^m+1 Z^m ( n−ℓ ∑ q=1 t_q² +∞ ∫ 0 s^2ℓ+2q+m e^−s ds + 2 n−ℓ ∑ q=2 q−1 ∑ p=1 (−1)^p+q t_pt_q +∞ ∫ 0 s^2ℓ+p+q+m e^−s ds )
<r^m>_n.ℓ = n^m−1 (n − ℓ − 1)! (n + ℓ)! 2^m+1 Z^m ( n−ℓ ∑ q=1 t_q² (2ℓ + 2q + m)! + 2 n−ℓ ∑ q=2 q−1 ∑ p=1 (−1)^p+q t_pt_q (2ℓ + p + q + m)! )

(E7.6)

where the identity α = Z n has been used. For ℓ = n − 1, only the term with q = 1, i.e. t₁² (2ℓ + 2 + m)! = (2n + m)!, survives, so that you have

<r^m>_n.n−1 = n^m (2n + m)! (2n)! 2^m Z^m

(E7.7)

e.g.

<r>₁₀ = 3 2 Z, <r>₂₁ = 5 Z, <r>₃₂ = 21 2 Z, <r>₄₃ = 18 Z, …

(E7.8)

and

<r²>₁₀ = 3 Z², <r²>₂₁ = 30 Z², <r²>₃₂ = 126 Z², <r²>₄₃ = 360 Z², …

(E7.9)

For ℓ = n − 2, the survivors are the terms with q = 1 and 2, i.e.

t₁² (2ℓ + 2 + m)! = 4 (n − 1)² (2n + m − 2)!
t₂² (2ℓ + 4 + m)! = (2n + m)! = (2n + m) (2n + m − 1) (2n + m − 2)!
− 2t₁t₂ (2ℓ + 3 + m)! = − 4 (n − 1) (2n + m − 1)! = − 4 (n − 1) (2n + m − 1) (2n + m − 2)!

so that you have

<r^m>_n.n−2 = n^m−1 (2n + m − 2)! [2n + m(m + 3)] (2n − 2)! 2^m+1 Z^m

(E7.10)

e.g.

<r>₂₀ = 6 Z, <r>₃₁ = 25 2 Z, <r>₄₂ = 21 Z, …

(E7.11)

and

<r²>₂₀ = 42 Z², <r²>₃₁ = 180 Z², <r²>₄₂ = 504 Z², …

(E7.12)

However, after all this math, it is comfortable to verify that, for m = 1 and 2, eq (E7.6) can be put in the form of eqs (E7.13) and (E7.14)

<r>_n,ℓ = 3n² − ℓ(ℓ + 1) 2Z

(E7.13)

<r²>_n,ℓ = n² [ 5 n² − 3 ℓ(ℓ + 1) + 1 ] 2 Z²

(E7.14)

The standard deviation, i.e. the square root of the variance, of the electron's distribution in the radial direction, σ_r;n,ℓ, has the following expression:

σ_r;n,ℓ = √<r²>_n,ℓ − <r>_n,ℓ² = √ n² (n² + 2) − ℓ² (ℓ + 1)² 2 Z

(E7.15)

An alternative solution formula for the integral in eq. (E7.3) is reported in the literature.[9Poh-Aun Lee, Seng-Huat Ong, H. M. Srivastava
Intern. J. Computer Math. 2001, 78, 303-321, equation 18., LL3ResearchGate online resource: “Some Integrals of the Products of Laguerre Polynomials”.]

Setting ω = n^m−1 (n − ℓ − 1)! (n + ℓ)! 2^m+1 Z^m , eq (E7.3) can be rewritten as

ω⁻¹ <r^m>_n.ℓ = +∞ ∫ 0 s^2ℓ+m+2 [L^2ℓ+1_n−ℓ−1(s)]² e^−s ds
ω⁻¹ <r^m>_n.ℓ = (2ℓ + m + 2)! n−ℓ−1 ∑ q=0 ( m + 1 n − ℓ − q − 1 )^{^²} ( 2ℓ + m + q + 1 q )

where the solution formula of the integral is taken from reference [9Poh-Aun Lee, Seng-Huat Ong, H. M. Srivastava
Intern. J. Computer Math. 2001, 78, 303-321, equation 18., LL3ResearchGate online resource: “Some Integrals of the Products of Laguerre Polynomials”.] Developing the formula yields

ω⁻¹ <r^m>_n.ℓ = ( (m + 1)! (n − ℓ − 1)! (ℓ + m − n + 2)! )^{^²} (2ℓ + m +2)!
ω⁻¹ <r^m>_n.ℓ + ( (m + 1)! (n − ℓ − 2)! (ℓ + m − n + 3)! )^{^²} (2ℓ + m + 3)! 1!
ω⁻¹ <r^m>_n.ℓ + ( (m + 1)! (n − ℓ − 3)! (ℓ + m − n + 4)! )^{^²} (2ℓ + m + 4)! 2!
ω⁻¹ <r^m>_n.ℓ + …
ω⁻¹ <r^m>_n.ℓ + ( (m + 1)! (n − ℓ − q − 1)! (m + ℓ − n + q + 2)! )^{^²} (2ℓ + m + q + 2)! q!
ω⁻¹ <r^m>_n.ℓ + …
ω⁻¹ <r^m>_n.ℓ + ( (m + 1)! m! )^{^²} (n + ℓ + m)! (n − ℓ − 2)!
ω⁻¹ <r^m>_n.ℓ + (n + ℓ + m + 1)! (n − ℓ − 1)!

The summation involves only the first term for ℓ = n − 1, which allows to derive <r^m>₁₀, <r^m>₂₁, <r^m>₃₂, <r^m>₄₃, etc. For ℓ = n − 2, the summation extends to the first two terms, allowing to recover <r^m>₂₀, <r^m>₃₁, <r^m>₄₂, and so on for any pair (n,ℓ).

Using Slater-type orbitals. If eq. (E7.2) is written in terms of STOs, it yields

<r^m>_n = +∞ ∫ 0 r^m+2 |R_n(r)|² dr = (2ζ)²ⁿ⁺¹ (2n)! +∞ ∫ 0 r^2n+m e^{− 2 ζ r} dr = (2n + m)! (2n)! (2ζ)^m

(E7.16)

where the last equality is justified by eq. (E2.5). Eq. (E7.16) can be rewritten explicitly for cases where m = 1 or 2:

<r>_n = 2n + 1 2ζ

(E7.17)

<r²>_n = (2n + 1) (2n + 2) 4 ζ²

(E7.18)

The standard deviation, i.e. the square root of the variance, of the electron's distribution in the radial direction, σ_r;n, has the following expression:

σ_r;n = √<r²>_n − <r>_n² = √ 2n + 1 2 ζ

(E7.19)

From eqs (E7.17) and (E7.19) it follows that the relative error on the average distance of the electron from the nucleus is σ_r;n / <r>_n = 1 / √ 2n + 1 , which for n = 1 is equal to 57.7%

The numerical values of first and second moments with the associated standard deviation, calculated by means of eqs (E7.13-15) and (E7.17-19), are compared in Table E7.1.

**Table E7.1** - First and second moments of the electron's distribution in the radial direction, and associated standard deviation for hydrogenic orbitals and Slater-type orbitals (ζ = Z).
n,ℓ	exact hydrogenic orbitals			Slater-type orbitals
n,ℓ	Z <r>_n,ℓ	Z² <r²>_n,ℓ	Z σ_r;n,ℓ	ζ <r>_n	ζ² <r²>_n	ζ σ_r;n
1,0	1.5	3	0.87	1.5	3	0.87
2,0	6	42	2.45	2.5	7.5	1.12
2,1	5	30	2.24	2.5	7.5	1.12
3,0	13.5	207	4.97	3.5	14	1.32
3,1	12.5	180	4.87
3,2	10.5	126	3.97
4,0	24	648	8.49	4.5	22.5	1.50
4,1	23	600	8.43
4,2	21	504	7.94
4,3	18	360	6.00

Exercise 8: compare the most probable distances of the electron from the proton in the hydrogen 1s, 2s and 2p states with the corresponding average radius. The most probable distance of the electron from the nucleus is the value of r which maximizes the radial probability density ρ_n,ℓ(r) = r² |R_n,ℓ(r)|². Since ρ_n,ℓ(r) is largest where r R_n,ℓ(r) reaches its maximum, we can look for the most probable r_max distance by setting

d [r R_n,ℓ(r)] dr = 0

(E8.1)

using the functions R_n,ℓ(r) from Teble E6.2. For the 1s state of hydrogen, the condition for a maximum is

d [r R_1s(r)] dr = d dr ( 2 √Z³ e^{−Z r} ) = 2 √Z³ e^{−Z r} (1 − Z r) = 0 ⇒ r_max = 1 Z

(E8.2)

The average or "expectation value" of the radius for the electron in the ground state of hydrogen was obtained in the Exercise 7 and is <r> = 3 2Z . It may seem a bit surprising that the average value of r is 1.5 times the most probable value. The extended tail of the probability density accounts for the average being greater than the most probable value.
For the 2s state of hydrogen, the condition for a maximum is

d [r R_2s(r)] dr = d dr ( √2 Z³ 4 (2r − Z r²) e^{−Z r/2} ) = √2 Z³ 8 (Z² r² − 6 Z r + 4) e^{−Z r/2} = 0 ⇒ r_max = 3 ± √5 Z

(E8.3)

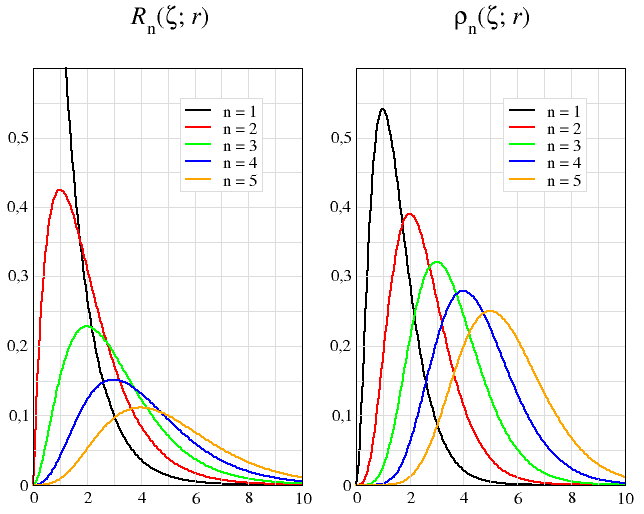
The two possible solutions indicate the presence of two humps in the radial probability density for the 2s orbital (cf the upper-right graph of Figure E6.3).

For the 2p state of hydrogen, a similar analysis yields,

d [r R_2s(r)] dr = d dr ( √6 Z⁵ 12 r² e^{−Z r/2} ) = √6 Z⁵ 24 (4 r − Z r²) e^{−Z r/2} = 0

(E8.4)

with the obvious roots r_min = 0 and r_max = 4 / Z. Thus, the most probable distances of the electron from the nucleus for the 1s and 2p states are the same predicted by the simple Bohr model for the radius of the first and second orbits. As in the case of the ground state, the most probable value of r in the 2s and 2p states is lower than the average value.

As usual, it is worth to compare the results for the hydrogenic orbitals with those that can be obtained using Slater-type orbitals:

d [r R_n(r)] dr = d dr ( √ (2ζ)²ⁿ⁺¹ (2n)! rⁿ e^{−ζ r} ) = √ (2ζ)²ⁿ⁺¹ (2n)! rⁿ⁻¹ (n − ζ r) e^{−ζ r} = 0

(E8.5)

with the obvious roots r_min = 0 and r_max = n / ζ (cf the graph on the right in Figure E6.4). Again the value of r_max is lower than the average value and the following relationship holds:

r_max,n = 2 n 2 n + 1 <r>_n

(E8.6)

Exercise: Find the moment generating function of an exponential random variable r with parameter ζ, e.g. the radial density function of the gound state of the hydrogen atom (click to view/hide details).

If the radial density function of the ground state of the hydrogen atom is ρ(r) = γ³ 2 r² e^{−γ r}, where γ = 2 ζ, the moment generating function is by definition:

M_r(s) = E(e^{s r}) = +∞ ∫ 0 e^{s r} ρ(r) dr = γ³ 2 +∞ ∫ 0 e^−(γ−s)r r² dr = γ³ (γ − s)³

provided that s < γ. Note that M_r(s)❘_s=0 = 1 is the normalization condition of the radial density function ρ(r). It's now easy to verify that the n-th derivative of M_r(s) with respect to s (n times),

dⁿ d sⁿ M_r(s) = dⁿ d sⁿ [γ (γ − s)⁻¹]³ = n! 2 (γ − s)ⁿ

calculated at s = 0, equals the n-th moment of ρ(r):

dⁿ d sⁿ M_r(s)❘_s=0 = n! 2 γⁿ.

Indeed, the n-th moment of ρ(r) is by definition:

⟨rⁿ⟩ ≡ E(rⁿ) = +∞ ∫ 0 rⁿ ρ(r) dr = γ³ 2 +∞ ∫ 0 e^{−γ r} rⁿ⁺² dr = n! 2 γⁿ.

Exercise: Use an 1s-GTO, as a trial function, to find an upper bound to the exact ground state energy of the hydrogen atom (click to view/hide details).

An 1s-GTO has the form

❘Φ⟩ = ( 2α π )^{^{^³⁄₄}} e^{−α r²}

(t)

and satisfies the normalization condition, ⟨Φ❘Φ⟩ = 1, i.e.

⟨Φ❘Φ⟩ = ( 2α π )^{^{^³⁄₂}} +∞ ∫ 0 e^{−2α r²} r² dr π ∫ 0 sinθ dθ 2π ∫ 0 dφ
⟨Φ❘Φ⟩ = ( 2α π )^{^{^³⁄₂}} ⋅ π^½ 4 (2 α)^{^3/2} ⋅ 4 π = 1

(u)

The ground state energy, eq.(14), is then given by

E = ⟨ Φ❘− 1 2 d² d r² − 1 r d d r − Z r ❘Φ ⟩ = ⟨ Φ❘− 2 α² r² + 3 α − Z r ❘Φ ⟩
E = 4 π ( 2α π )^{^{^³⁄₂}} ( − 2 α² +∞ ∫ 0 e^{−2α r²} r⁴ dr + 3 α +∞ ∫ 0 e^{−2α r²} r² dr − Z +∞ ∫ 0 r e^{−2α r²} dr )
E = 4 π ( 2α π )^{^{^³⁄₂}} [ 3 16 ( π 2 α )^{^{^¹⁄₂}} − Z 4 α ]
E = 1 2 ( 3 α − 8 Z √ α 2 π )

(v)

where the values of the following definite integrals,[3“A Concise Handbook of Mathematics, Physics, and Engineering Sciences”
Polyanin, A. D., Chernoutsan, A. I., Eds.
Taylor & Francis Group: New York, 2011.] +∞ ∫ 0 r²ⁿ e^{−γ
r²} dr = (2 n − 1)!! 2ⁿ⁺¹ γⁿ ( π γ )^{^{^¹⁄₂}} = (2 n)! 2²ⁿ⁺¹ n! γⁿ ( π γ )^{^{^¹⁄₂}} and +∞ ∫ 0 r²ⁿ⁺¹ e^{−γ
r²} dr = n! 2 γⁿ⁺¹ , have been used. The optimal value of the exponent α is obtained by solving the equation d E d α = 0, i.e.

3 − 4 Z √ 2 π α = 0 ⇒ α = 8 Z² 9 π = 0.28294246 Z²

(w)

Back substituting this value of the exponent α into the last equality of eq. (v) we find that E = − 4 Z² 3 π = −0.42441369 Z² hartree is an upper bound to the exact ground state energy (which is -0.5 hartree).[2Szabo, A.; Ostlund, N. S.
“Modern Quantum Chemistry - Introduction to Advanced Electronic Structure Theory”
Macmillan Publishing Co., Inc., New York, 1982, p. 33.] Finally, the normalization constant becomes

( 2α π )^{^{^³⁄₄}} = 8 ( Z 3 π )^{^{^³⁄₂}} = 0.27649271 Z^3/2

(x)

and the adial density function of the ground state of the hydrogen atom is

ρ_1s(r) = 64 27 ( Z π )^{^³} r² exp ( − 16 Z² 9 π r² )

(y)

Exercise: Write the wave function files (.wfn) for the hydrogen atom using both Slater and Gaussian basis sets (click to view/hide details).

1) Slater basis set (a single 1s orbital, according to eq.16):


Name  H     Run Type  SinglePoint    Method  ROHF     Basis Set  Slater
SLATER                1 MOL ORBITALS      1 PRIMITIVES        1 NUCLEI
  H         (CENTRE  1)   0.00000000  0.00000000  0.00000000  CHARGE =  1.0
CENTRE ASSIGNMENTS    1
TYPE ASSIGNMENTS      1
EXPONENTS  1.0000000E+00
MO  1                     OCC NO =   1.00000000 ORB. ENERGY =  -0.5
  0.56418958E+00
END DATA
 THE SCF ENERGY =     -0.500000000000 THE VIRIAL(-V/T)=   2.00000000

2) Gaussian basis set (a single 1s orbital, according to eq.D?):


Name  H     Run Type  SinglePoint    Method  ROHF     Basis Set  STO-1G
GAUSSIAN              1 MOL ORBITALS      1 PRIMITIVES        1 NUCLEI
  H         (CENTRE  1)   0.00000000  0.00000000  0.00000000  CHARGE =  1.0
CENTRE ASSIGNMENTS    1
TYPE ASSIGNMENTS      1
EXPONENTS  0.2829425E+00
MO  1                     OCC NO =   1.00000000 ORB. ENERGY =  -0.42441369
  0.27649271E+00
END DATA
 THE SCF ENERGY =     -0.424413690000 THE VIRIAL(-V/T)=   2.00000000

References

“Exact Gaussian Expansions of Slater-Type Atomic Orbitals”
Gomes, A. S. P.; Custodio, R. J. Comput. Chem. 2002, 23, 1007-1012.
Szabo, A.; Ostlund, N. S. “Modern Quantum Chemistry − Introduction to Advanced Electronic Structure Theory” Macmillan Publishing Co., Inc., New York, 1982, p. 33. ISBN 0-02-949710-8.
“A Concise Handbook of Mathematics, Physics, and Engineering Sciences”; Polyanin, A. D., Chernoutsan, A. I., Eds.; Taylor & Francis Group: New York, 2011.
A. V. Arecchi, T. Messadi, and R. J. Koshel, “Field Guide to Illumination”, SPIE Press, Bellingham, WA, 2007, p. 2. ISBN: 9780819467683.
Leonard I. Schiff, “Quantum Mechanics”. McGraw-Hill, 1968, Chapter 16, pp. 88-99. ISBN-13: 9780070856431. ISBN-10: 0070856435.
Paul A. Tipler; Gene Mosca; “Physics for Scientists and Engineers: Extended Version”. W. H. Freeman, 2003, Section 36-4, p. 1181. ISBN-13: 9780716743897. ISBN-10: 0716743892.
David A. B. Miller, “Quantum Mechanics for Scientists and Engineers”. Cambridge University Press, 2008, Chapter 10, pp. 259-278. ISBN-13: 9780521897839. ISBN-10: 0521897831.
Milton Abramowitz and Irene A. Stegun, eds. “Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables”. United States Government Printing Office, 1972, § 22.3, p. 775. ISBN-13: 9780318117300. ISBN-10: 0318117304.
“Some Integrals of the Products of Laguerre Polynomials”
Lee, P.-A.; Ong, S.-H.; Srivastava, H. M. Intern. J. Computer Math. 2001, 78, 303-321, equation 18. DOI: 10.1080/00207160108805112
Einstein, A.; Infeld, L. “The Evolution of Physics” Cambridge University Press, 1971, p. 106, ISBN 0-521-09687-1. Internet Archive: accessed February 24, 2019.

Notes

Probability amplitude. In classical physics a wave describe "the motion of something which is not matter, but energy propagated through matter".[last1Albert Einstein, Leopold Infeld, “The Evolution of Physics”
Cambridge University Press, 1971, p. 106.] Not all waves require a medium, as electromagnetic waves and gravitational waves can travel through a vacuum. Waves are characterized by properties like the wavelength, the frequency, and the amplitude. The intensity of light or sound is found to be proportional to the amplitude of the associated wave. “When Schrödinger first discovered the correct laws of quantum mechanics, he wrote an equation which described the amplitude to find a particle in various places. This equation was very similar to the equations that were already known to classical physicists − equations that they had used in describing the motion of air in a sound wave, the transmission of light, and so on.”[LL4“The Feynman Lectures on Physics”, Online Edition, Vol. III, Ch. 3: “Probability Amplitudes”] Then Max Born postulated that the probability of finding a particle in some region is proportional to the square of the modulus of the wave function (Born rule).[LL5Born, M. “The statistical interpretation of quantum mechanics”, Nobel lecture, December 11, 1954.] So the term (probability) amplitude can be used for the wave function.

Volume element in spherical coordinates.

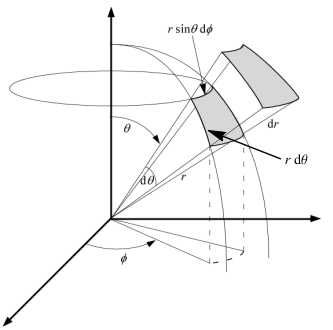
Working in spherical coordinates, the diagram on the left enable us to calculate the infinitesimal volume element as

dV = dr ⋅ r dθ ⋅ r sinθ dφ = r² sinθ dr dθ dφ

The volume of a solid is always given by the integration of the infinitesimal volume element dV over the entire solid. We cover a sphere of radius R if we let r ∈ [0,R], θ ∈ [0,π], and φ ∈ [0,2π]. The volume of the sphere is then given by

V = ∫ sphere dV = R ∫ 0 r² dr π ∫ 0 sinθ dθ 2π ∫ 0 dφ
V = [ 1 3 r³ ]^{^{^R}}₀ ⋅ [−cosθ ]^{^{^π}}₀ ⋅ [φ ]^{^{^2π}}₀

V = 4 π R³ 3

Surface area element in spherical coordinates. The diagram of the previous note [N1] also enables us to calculate the infinitesimal area elements when we integrate over only two of the spherical coordinates. When we integrate over the surface of a sphere, we only vary θ and φ by dθ and dφ, respectively, and we do not vary r at all. The corresponding area element is given in the diagram of the previous note as

dA = r² sinθ dθ dφ

The surface area of a sphere of radius R is obtained by direct integration over the entire sphere, letting θ ∈ [0,π] and φ ∈ [0,2π] while using the spherical coordinate area element R² sinθ dθ dφ,

A = ∫ sphere dA = R² π ∫ 0 sinθ dθ 2π ∫ 0 dφ
A = R² ⋅ [−cosθ ]^{^{^π}}₀ ⋅ [φ ]^{^{^2π}}₀

A = 4 π R²

Solid angle. A solid angle is the 3 dimensional analog of an ordinary angle. It is related to the surface area of a sphere in the same way an ordinary angle is related to the circumference of a circle.

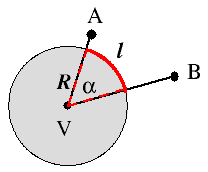
A plane angle, α, is made up of the lines that from two points A and B meet at a vertex V: it is defined by the arc length (red curve in the figure on the left) of a circle subtended by the lines and by the radius R of that circle (dotted red lines),[4A. V. Arecchi, T. Messadi, and R. J. Koshel
“Field Guide to Illumination”
SPIE Press, Bellingham, WA, 2007, p. 2.] as shown on the left. The dimensionless unit of plane angle is the radian. The value in radians of a plane angle α is the ratio

α = ℓ R

of the length ℓ of a circular arc to its radius R. It follows that the plane angle subtended by the full circle measures 2π radians.

Si definisce angolo solido ciascuna delle due regioni in cui viene suddiviso lo spazio dalla superficie formata dalle semirette passanti per uno stesso punto (detto vertice dell'angolo solido) e per i punti di una curva chiusa semplice tracciata su una superficie non contenente il vertice. L'unità di misura dell'angolo solido Ω è lo steradiante. La misura in steradianti dell'angolo solido Ω è definita dal rapporto Ω = A/R² tra l'area A della porzione di superficie sferica di raggio R vista sotto l'angolo Ω e il quadrato del raggio, ed è indipendente dal particolare valore del raggio scelto. L'angolo solido sotteso da una superficie generica rispetto a un punto P è dunque equivalente a quello sotteso dalla proiezione della stessa superficie su una sfera di raggio qualsiasi centrata in P. Dalla precedente definizione consegue che l'angolo solido sotteso dall'intera superficie sferica misura 4π. Per avere la misura in gradi quadrati si moltiplica il valore in steradianti per (180/π)², ovvero per 3282,8 (circa). Quindi tutta la sfera corrisponde a circa 41253 gradi quadrati.
A solid angle is made up from all the lines that from a closed curve meet at a vertex: it is defined by the surface area A of a sphere subtended by the lines and by the radius R of that sphere,[4A. V. Arecchi, T. Messadi, and R. J. Koshel
“Field Guide to Illumination”
SPIE Press, Bellingham, WA, 2007, p. 2.] as shown in the Figure on the right. The dimensionless unit of solid angle is the steradian. The measure in steradians of a solid angle Ω is the area A on the surface of a sphere of radius R divided by the radius squared,

Ω = A R² ,

and is independent of the particular value of the chosen radius. Because the area A of the entire spherical surface is 4πr², the definition implies that a sphere subtends 4π steradians at its center. By the same argument, the maximum solid angle that can be subtended at any point is 4π steradians.
Concisely, the solid angle Ω subtended by a surface S is defined as the surface area Ω of a unit sphere covered by the surface’s projection onto the sphere.[L4Weisstein, E. W. "Solid Angle,"
From MathWorld - A Wolfram Web Resource.] That’s a very complicated way of saying the following: You take a surface, like the bright red circle in the figure on the right. Then you project the edge of the circle (but in general it could be any closed curve) to the center of a sphere of any radius R. The projection intersects the sphere and forms a surface area A. Then you calculate the surface area of your projection and divide the result by the radius squared. That's it.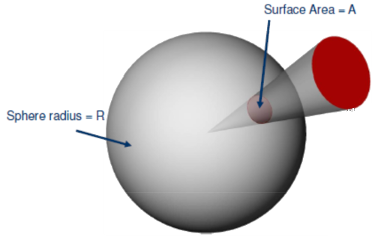

The infinitesimal element of a solid angle Ω is given by dΩ = dA R² , where dA is the surface area element in spherical coordinates defined in [N2Surface area element in spherical coordinates.], so that

dΩ = sinθ dθ dφ

is equal to the differential surface area on the unit sphere. Its integral over the solid angle of all space being subtended is the surface area of the unit sphere, which is 4 π steradians.[L4Weisstein, E. W. "Solid Angle,"
From MathWorld - A Wolfram Web Resource., L5Wikipedia contributors, "Solid angle,"
Wikipedia, The Free Encyclopedia.]

Ω = ∫ Ω dΩ = π ∫ 0 sinθ dθ 2π ∫ 0 dφ = [−cosθ ]^{^{^π}}₀ ⋅ [φ ]^{^{^2π}}₀ = 4 π

Volume of a spherical shell of infinitesimal thickness. Consider two spheres, both centered in the origin: the inner with radius r and the outer with radius r + dr. To compute the volume of the spherical shell between their two surfaces, proceed as follows:

dV	= 4 / 3 π (r + dr)³ − 4 / 3 π r³
	= 4 / 3 π (r³ + 3r²dr + 3r dr² + dr³ − r³	(N1.1)
	= 4 / 3 π (3r²dr + 3r dr² + dr³)
	≈ 4 π r²dr

where, in the last equality, the terms drⁿ with n > 1 have been neglected. In a different way, using differentiation of volume V = 4 3 π r³ w.r.t. radius, you get area (rate of change of volume is area)

d V d r = 4 π r² ⇒ d V = 4 π r² d r

(N1.2)

U-substitution. Many pages on the Web are dedicated to the method of integration by substitution, also known as the u-substitution. Among these, we remember the page of Wikipedia.[L6Wikipedia contributors, "Integration by substitution,"
Wikipedia, The Free Encyclopedia.] The u-substitution is also described in some pages of the PAMoC manual, in particular in section 4.7 of the chapter on "Charge Distributions"“Transformation of the Random Vector Variable”
PAMoC Manual: Charge Distributions, Section 4.7, and in sections 1.5 and 2.3 of the chapter on "Methods of Numerical Integration" “Transformation of coordinates” (section 1.5)
“Radial integral and transformation of the radial coordinate” (section 2.3)
PAMoC Manual: Methods of Numerical Integration..
Remember that ∫ f '(x) e^f(x) dx = e^f(x) + C.

Real Spherical Harmonics. Orthonormalized Laplace’s spherical harmonics are defined as

Y_ℓ^m(θ,φ) = (−1)^m N_ℓm P_ℓ^m(cosθ) e^imφ

(N7.1)

where P_ℓ^m(cosθ) is the associate Legendre polynomial of degree ℓ and order m ( ℓ ≥ 0 and −ℓ≤ m ≤ ℓ). Spherical harmonics are single-valued, smooth (infinitely differentiable), complex functions of two variables, θ and φ, indexed by two integers, ℓ and m, and form a complete set of orthonormal functions:

2π ∫ 0 dφ π ∫ 0 Y_ℓ^m(θ,φ) Y_ℓ'^m'*(θ,φ) sinθ dθ = δ_ℓℓ' δ_mm'

(N7.2)

This normalization is used in quantum mechanics because it ensures that probability is normalized, i.e. π ∫ 0 |Y_ℓ^m(Ω)|² dΩ = 1, with dΩ = sinθ dθ and normalization factor:

N_ℓm = √ 2ℓ + 1 4 π ⋅ (ℓ − |m|)! (ℓ + |m|)!

(N7.3)

The real forms of the spherical harmonics, also known as tesseral harmonics, are obtained by taking the linear combinations [Y_ℓ^m(θ,φ) ± Y_ℓ^−m(θ,φ)]/√2. They are defined as follows

Y_ℓm(θ,φ) = M_ℓm U_ℓm(θ,φ)

(N7.4)

where

U_ℓm(θ,φ) = P_ℓ^|m|(cosθ) { cos(|m|φ), m ≥ 0 sin(|m|φ), m < 0

(N7.5)

are the un-normalized tesseral harmonics, and M_ℓm is the normalization factor

M_ℓm = N_ℓm √ 2 − δ_|m|,0 = √ 2ℓ + 1 4 π ⋅ (2 − δ_|m|,0) ⋅ (ℓ − |m|)! (ℓ + |m|)!

(N7.6)

Links

Euler integrals. Encyclopedia of Mathematics. URL: https://www.encyclopediaofmath.org/index.php?title=Euler_integrals&oldid=25725 (accessed January 16, 2019.
Wikipedia contributors, "Gamma function," Wikipedia, The Free Encyclopedia.
https://en.wikipedia.org/w/index.php?title=Gamma_function&oldid=878188592 (accessed January 16, 2019).
Weisstein, Eric W. "Gamma Function." From MathWorld − A Wolfram Web Resource.
http://mathworld.wolfram.com/GammaFunction.html (accessed January 16, 2019).
Weisstein, Eric W. "Reflection Relation." From MathWorld − A Wolfram Web Resource.
http://mathworld.wolfram.com/ReflectionRelation.html (accessed January 17, 2019).
Weisstein, Eric W. "Leibniz Integral Rule." From MathWorld − A Wolfram Web Resource. http://mathworld.wolfram.com/LeibnizIntegralRule.html (accessed January 17, 2019).
Weisstein, Eric W. "Multifactorial." From MathWorld − A Wolfram Web Resource.
http://mathworld.wolfram.com/Multifactorial.html (accessed January 19, 2019).
Wikipedia contributors, "Particular values of the gamma function," Wikipedia, The Free Encyclopedia.
https://en.wikipedia.org/w/index.php?title=Particular_values_of_the_gamma_function&oldid=874045399 (accessed January 18, 2019).
Wikipedia contributors, "Spherical harmonics." Wikipedia, The Free Encyclopedia.
https://en.wikipedia.org/wiki/Spherical_harmonics (accessed October 3, 2018).
Wikipedia contributors, "Table of spherical harmonics." Wikipedia, The Free Encyclopedia.
https://en.wikipedia.org/wiki/Table_of_spherical_harmonics (accessed October 3, 2018).
Weisstein, Eric W. “Spherical Harmonic.” From MathWorld − A Wolfram Web Resource.
http://mathworld.wolfram.com/SphericalHarmonic.html (accessed October 3, 2018).
Weisstein, Eric W. “Solid Angle.” From MathWorld − A Wolfram Web Resource.
http://mathworld.wolfram.com/SolidAngle.html (accessed October 4, 2018).
Wikipedia contributors, “Solid angle.” Wikipedia, The Free Encyclopedia.
https://en.wikipedia.org/wiki/Solid_angle (accessed October 4, 2018).
Wikipedia contributors, “Integration by substitution.” Wikipedia, The Free Encyclopedia.
https://en.wikipedia.org/wiki/Integration_by_substitution (accessed October 12, 2018).
Mark E. Tuckerman, “The Schrödinger equation for the hydrogen atom and hydrogen-like cations”, 2011-10-26.
(Lecture 8: CHEM-UA 127: Advanced General Chemistry I)
http://www.nyu.edu/classes/tuckerman/adv.chem/lectures/lecture_8/node5.html (accessed October 31, 2018).
“Solid Angle”. Optipedia: SPIE Press books opened for your reference. Excerpt from “Field Guide to Illumination” by Angelo V. Arecchi, Tahar Messadi, R. John Koshel.[4A. V. Arecchi, T. Messadi, and R. J. Koshel
“Field Guide to Illumination”
SPIE Press, Bellingham, WA, 2007, p. 2.]
http://spie.org/publications/fg11_p02_solid_angle (accessed November 12, 2018).
Rudi Winter, “Solving Schrödinger's equation for the hydrogen atom”
http://users.aber.ac.uk/ruw/teach/237/hatom.php (Accessed February 18, 2019).
“GRACE: GRaphing, Advanced Computation and Exploration of data”. Online resource: http://plasma-gate.weizmann.ac.il/Grace/. Accessed February 7, 2019.
“Some Integrals of the Products of Laguerre Polynomials”
Lee, P.-A.; Ong, S.-H.; Srivastava, H. M. Intern. J. Computer Math. 2001, 78, 303-321, equation 18.
Online resource: https://www.researchgate.net/publication/233359915_Some_Integrals_of_the_products_of_laguerre_polynomials. Accessed February 13, 2019.
“The Feynman Lectures on Physics”, Online Edition, Vol. III, Ch. 3: “Probability Amplitudes”.
www.feynmanlectures.caltech.edu/III_03.html (accessed Febrary 24, 2019).
Born, M. “The statistical interpretation of quantum mechanics”. Nobel lecture, December 11, 1954. Online resource (PDF): www.nobelprize.org/uploads/2018/06/born-lecture.pdf. Accessed February 24, 2019.
“Again an idea of Einstein's gave me the lead. He had tried to make the duality of particles - light quanta or photons - and waves comprehensible by interpreting the square of the optical wave amplitudes as probability density for the occurrence of photons. This concept could at once be carried over to the ψ-function: |ψ|² ought to represent the probability density for electrons (or other particles).”