Methods of Numerical Integration.

A survey of the numerical integration methods used in PAMoC is presented in this section of the manual.

Numerical estimation of integrals
Volume integral
Lebedev angular quadrature
Gauss-Legendre quadrature
Gauss-Laguerre quadrature
Generalized Gauss-Laguerre quadrature
Gauss-Hermite quadrature
Gauss-Chebyshev quadrature of the second kind
Gauss-Gill quadrature
Evenly spaced quadrature: the extended or composite trapezoidal rule
Tests of radial grid accuracies
Concluding Remarks
References
Notes
Links

1. - Numerical estimation of integrals

The basic problem in numerical integration is to compute an approximate solution to a definite integral of a function f(q) as a weighted sum of function values at specified points within the domain of integration:

b ∫ a f(q) dq ≈ n ∑ i=1 w_i f(q_i)

(1.1)

A natural way to approximate the integral (1.1) is to find a polynomial L_n(f; q₁, q₂, ..., q_n; q) of degree at most (n − 1) that interpolates f(q) in n distinct points q₁, q₂, ..., q_n in [a, b], i.e. such that

L_n(q_i) = f(q_i) ∀ i = 1, 2, ..., n

(1.2)

and then write

b ∫ a f(q) dq ≈ b ∫ a L_n(f; q₁, q₂, ..., q_n; q) dq

(1.3)

Given a basis l₁, l₂, ..., l_n of the space of polynomials of degree less or equal to (n − 1), we write

L_n(q) = a₁ l₁(q) + a₂ l₂(q) + ... + a_n l_n(q)

(1.4)

and find the coefficients a₁, a₂, ..., a_n by solving the linear system

l₁(q₁)	l₂(q₁)	…	l_n(q₁)
l₁(q₂)	l₂(q₂)	…	l_n(q₂)
⋮	⋮		⋮
l₁(q_n)	l₂(q_n)	…	l_n(q_n)

a₁

a₂

⋮

a_n

f(q₁)

f(q₂)

⋮

f(q_n)

(1.5)

We choose, as a basis, the Lagrange polynomials of degree (n − 1)

l_i(q) = n ∏ k=1
k≠i q − q_k q_i − q_k

(1.6)

which satisfy the condition

l_i(q_j) = δ_ij

(1.7)

where δ_ij is the Kronecker delta. Because of this condition, the matrix in eq. (1.5) is equal to the identity matrix and a_i = f(q_i) ∀ i. Therefore, the interpolating polynomial (1.4) is given by

L_n(q) = n ∑ i=1 l_i(q) f(q_i)

(1.8)

This makes L_n(q) a polynomial of degree (n − 1) with L_n(q_j) = n ∑ i=1 δ_ij f(q_i) = f(q_j). Inserting the expression (1.8) for L_n(q) into eq. (1.3), gives the quadrature rule (1.1), with

w_i = b ∫ a l_i(q) dq

(1.9)

1.1. - Newton-Cotes quadrature formulas. The interpolatory procedure outlined above leads to an extremely useful and straightforward family of numerical integration techniques, which are known as Newton-Cotes formulas and apply to n equispaced quadrature points or nodes in the range [a, b], such that q_k = a + (k − 1) h for k = 1, 2, ..., n and step size h ≡ (b − a)/(n − 1). Newton-Cotes formulas may be "closed" if all points in the interval [a = q₁, b = q_n] are used, "open" if only the points [q₂, q_n−1] are used, or a variation of these two. A few closed Newton-Cotes quadrature formulas for small values of n are reported in Table 1.1.

**Table 1.1.** - Closed Newton-Cotes quadrature formulas for n = 2, 3, 4, 5 points *q_i* equally spaced by h = q_i+1 − *q_i* = (b − a)/(n − 1), so *f_i* = f(*q_i*) ∀ 1 ≤ i ≤ n.
n	L_n(q) = n ∑ i=1 l_i(q) f_i	b ∫ a L_n(q) dq = n ∑ i=1 f_i b ∫ a l_i(q) dq	formula type
2	q − q₂ / q₁ − q₂ f₁ + q − q₁ / q₂ − q₁ f₂ = f₂ − f₁ / q₂ − q₁ q + q₂ f₁ − q₁ f₂ / q₂ − q₁	1 / 2 f₂ − f₁ / q₂ − q₁ (q₂² − q₁²) + q₂ f₁ − q₁ f₂ / q₂ − q₁ (q₂ − q₁) = 1 / 2 (q₂ − q₁) (f₁ + f₂) = 1 / 2 h (f₁ + f₂)	trapezoidal rule
3	(q − q₂) (q − q₃) / (q₁ − q₂) (q₁ − q₃) f₁ + (q − q₁) (q − q₃) / (q₂ − q₁) (q₂ − q₃) f₂ + (q − q₁) (q − q₂) / (q₃ − q₁) (q₃ − q₂) f₃	1 / 3 h (f₁ + 4 f₂ + f₃)	Simpson's rule
4	(q − q₂) (q − q₃) (q − q₄) / (q₁ − q₂) (q₁ − q₃) (q₁ − q₄) f₁ + (q − q₁) (q − q₃) (q − q₄) / (q₂ − q₁) (q₂ − q₃) (q₂ − q₄) f₂ + (q − q₁) (q − q₂) (q − q₄) / (q₃ − q₁) (q₃ − q₂) (q₃ − q₄) f₃ + (q − q₁) (q − q₂) (q − q₃) / (q₄ − q₁) (q₄ − q₂) (q₄ − q₃) f₄	3 / 8 h (f₁ + 3 f₂ + 3 f₃ + f₄)	Simpson's 3/8 rule
5	(q − q₂) (q − q₃) (q − q₄) (q − q₅) / (q₁ − q₂) (q₁ − q₃) (q₁ − q₄) (q₁ − q₅) f₁ + (q − q₁) (q − q₃) (q − q₄) (q − q₅) / (q₂ − q₁) (q₂ − q₃) (q₂ − q₄) (q₂ − q₅) f₂ + (q − q₁) (q − q₂) (q − q₄) (q − q₅) / (q₃ − q₁) (q₃ − q₂) (q₃ − q₄) (q₃ − q₅) f₃ + (q − q₁) (q − q₂) (q − q₃) (q − q₅) / (q₄ − q₁) (q₄ − q₂) (q₄ − q₃) (q₄ − q₅) f₄ + (q − q₁) (q − q₂) (q − q₃) (q − q₄) / (q₅ − q₁) (q₅ − q₂) (q₅ − q₃) (q₅ − q₄) f₅	2 / 45 h (7 f₁ + 32 f₂ + 12 f₃ + 32 f₄ + 7 f₅)	Boole's rule

Using polynomial interpolation with polynomials of high degree over a set of equispaced points may result in an oscillating pattern that magnifies near the ends of the interpolation points and is known as Runge's phenomenon.[1Runge, C.
Zeitschrift für Mathematik und Physik 1901, 46, 224-243.] This implies that going to higher degrees does not always improve accuracy. Runge's phenomenon can be avoided by using a composite or extended rule.

Closed "extended" rules use multiple copies of lower order closed rules to build up higher order rules. For n tabulated points, using the 2-point trapezoidal rule (n − 1) times and adding the results gives

b = q_n ∫ a = q₁ f(q) dq = n−1 ∑ i=1 q_i+1 ∫ q_i f(q) dq ≈ 1 2 n−1 ∑ i=1 (q_i+1 − q_i) (f_i + f_i+1) = h ( 1 2 f₁ + n−1 ∑ i=2 f_i + 1 2 f_n )

(1.10)

where h ≡ (b − a) / (n − 1) and q_i = a + h (i − 1). It can be shown that the error associated with the n-point closed extended trapezoidal rule can be expressed in terms of derivatives at the endpoints, according to the Euler-Maclaurin formula

b = q_n ∫ a = q₁ f(q) dq − h ( 1 2 f₁ + n−1 ∑ i=2 f_i + 1 2 f_n ) = m ∑ k=1 B_2k (2k)! h^2k [ f^(2k−1)(a) − f^(2k−1)(b) ] + E_m(f)

(1.11)

The numbers B_j that appear in eq. (1.11) are Bernoulli numbers (B₀ = 1, B₁ = −¹⁄₂, B₂ = ¹⁄₆, B₄ = −¹⁄₃₀, B₆ = ¹⁄₄₂, B₈ = −¹⁄₃₀, ... ; B₃ = B₅ = B₇ = B₉ = ... = 0), and the remainder E_m(f) is often small.

The extended trapezoidal rule is discussed in section 10 with reference to its use in PAMoC.

1.2. - Gaussian quadrature. An n-point Gaussian quadrature rule is developped by requiring that the evaluation points are the roots of a polynomial belonging to a class of orthogonal polynomials p₀(q), p₁(q), …, p_n−1(q), defined in some interval [a, b] and such that

p_i(q) is a polynomial of degree i;
the inner product of any two polynomials p_i(q) and p_j(q) with respect to a positive function ω(q), called a weighting function, is given by
<p_i|ω|p_j> ≔ b ∫ a ω(q) p_i(q) p_j(q) dq = δ_ij b ∫ a ω(q) p_i²(q) dq ≕ δ_ij <p_i|ω|p_i> (1.12)

In addition, if <p_i|ω|p_i> = 1, the polynomials are orthonormal. In particular, eq. (1.12) states that

b ∫ a ω(q) p_i(q) p₀(q) dq = 0

Since p₀(q) is a polynomial of degree zero, it must be a constant and does not affect the integral, so that we may write

b ∫ a ω(q) p_i(q) dq = 0 ∀ i > 0.

(1.13)

Consider the set of roots q₁, q₂, ..., q_n of the polynomial p_n(q). It is trivial to show that n ∑ i=1 v_i p_n(q_i) = 0 for any set of v_i's, because p_n(q_i) = 0 for all q_i. However it is possible to show that there exists a unique set of v_i's, for which all polynomials of order 1 ≤ k ≤ n simultaneously obey the relation

b ∫ a ω(q) p_k(q) dq = n ∑ i=1 v_i p_k(q_i) = 0.

(1.14)

This is done by solving the simultaneous set of equations

p₀(q₁)	p₀(q₂)	…	p₀(q_n)
p₁(q₁)	p₁(q₂)	…	p₁(q_n)
⋮	⋮		⋮
p_n−1(q₁)	p_n−1(q₂)	…	p_n−1(q_n)

v₁

v₂

⋮

v_n

∫_a^b ω(q) p₀(q) dq

⋮

(1.15)

It can be shown that the determinant of this square matrix is non zero, therefore, it is invertible, i.e., a unique solution exists.

Let's now project f(q) into the set of orthogonal polynomials p₀(q), p₁(q), …, p_n−1(q)

f(q) = ω(q) n ∑ k=0 c_k p_k(q)

(1.16)

where

c_k = b ∫ a f(q) p_k(q) dq b ∫ a ω(q) p_k²(q) dq

(1.17)

is an expansion coefficient. Integrating both sides of eq. (1.16) over the interval [a, b] yields:

b ∫ a f(q) dq = n ∑ k=0 c_k b ∫ a ω(q) p_k(q) dq eq. (1.14) = n ∑ k=0 c_k n ∑ i=1 v_i p_k(q_i) = n ∑ i=1 v_i n ∑ k=0 c_k p_k(q_i) eq. (1.16) = n ∑ i=1 w_i f(q_i)

(1.18)

where

w_i = v_i ω(q_i)

(1.19)

Eq. (1.18) shows that the projection of the integrand f(q) into a basis of orthogonal polynomials occurs implicitly, with no need to explicitly evaluate the expansion coefficients. It states that, given an integer n, we can find a set of weigths w_i and abscissas q_i such that the approximation (1.1) or (1.18) is exact if the integrand f(q) is a polynomial. Then formula (1.18) is suitable for integrands that are smooth and well-behaved, and the best results will be achieved if f(q) is approximately a low order polynomial.

Notice that the weight function ω(q) is not overtly visible in the integration formula (1.18). However, using eq. (1.19) and defining

f(q) = ω(q) g(q)

(1.20)

eq. (1.18) becomes

b ∫ a ω(q) g(q) dq ≈ n ∑ i=1 v_i g(q_i)

(1.21)

Eq. (1.21) states that, given ω(q) and given an integer n, we can arrange the choice of weights and abscissas to make the integral exact for a class of integrands "polynomials times some known function ω(q)" rather than for the usual class of integrands "polynomials." Again, the best results will be achieved if g(q) is approximately a low order polynomial. The function ω(q) can then be chosen to remove singularities from the desired integral. Eq. (1.21) represents the well known Gaussian quadrature formulas, that in the particular case of ω(q) = 1 assume the form of eq. (1.18). A few Gauss quadrature formulas for different choices of a, b, and ω(q) are reported in Table 1.2.

**Table 1.2.** Gauss quadrature formulas for different choices of a, b, and ω(q). The *q_i*'s are the roots of the polynomial, and the *w_i*'s are the corresponding weights.
ω(q)	Interval [a,b]	Orthogonal polynomials	weights	`radrule`
1	[-1, 1]	n-th Legendre polynomial P_n(q) = 1 / 2ⁿ ⌊n/2⌋ ∑ k=0 (−1)^k (2n − 2k)! / k! (n − k)! (n − 2k)! q^n−2k	w_i = 2 / (1 − q_i²) [P'_n(q_i)]² (i = 1,2,…,n)	10
(1 − q²)^½	[-1, 1]	n-th Chebyshev polynomial of the second kind U_n(q) = ⌊n/2⌋ ∑ k=0 (-1)^k ( n − k k ) (2q)^n−2k with analytical roots: q_i = cos ( i π / n + 1 ) (i = 1,2,…, n)	w_i = π / n + 1 (1 − q_i²) (i = 1,2,…, n)	20
ln²q	[0, 1]	Gill polynomials Q₀(q) = 1, Q₁(q) = 8q − 1, Q₂(q) = 7992q² − 4104q + 217, …	w_i (i = 1,2,…,n)	30
e^−q	[0, ∞]	n-th Laguerre polynomial L_n(q) = n ∑ k=0 (−1)^k / k! ( n / k ) q^k	w_i = q_i / (n + 1)² [L_n+1(q_i) ]² (i = 1,2,…, n)	40
q^α e^−q, α > −1	[0, ∞]	n-th Generalized Laguerre polynomial L_n^(α)(q) = n ∑ k=0 ( n + α n − k) (−1)^k / k! q^k	w_i (i = 1,2,…,n)	50
e^−q²	[−∞, ∞]	n-th Hermite polynomial H_n(q) = (−1)ⁿ e^q² dⁿ / dqⁿ e^−q²	w_i = 2ⁿ⁻¹ n! √π / n² [H_n−1(q_i) ]² (i = 1,2,…, n)	60

PAMoC uses John Burkardt's FORTRAN90 version of IQPACK routines[27Elhay, S.; Kautsky, J.
ACM Transactions on Mathematical Software 1987, 13, 399-415.] to estimate roots and weights of Gaussian quadrature rules.

1.3. - Degree of exactness of a quadrature rule. In the following, we will use I(f) to denote the integral over a finite interval [a, b] that appears in the left hand side of eq. (1.1) or (1.18), and Q_n(f) to denote a generic interpolatory quadrature rule over n points in the same interval [a, b], i.e. the summation in the right hand side of eq. (1.1) or (1.18). A quadrature rule for a function f is exact if I(f) = Q_n(f).

Definition. A quadrature rule has degree of exactness m if it renders exact results when the integrand is any polynomial of degree ≤ m but not exact for at least one polynomial of degree (m + 1).

Independently of the choice of nodes, the degree of exactness of an n-point Newton-Cotes rule is ≤ (n − 1). In other words, this rule gives exact results for polynomials of degree ≤ (n − 1).

The quadrature rule of the form (1.1) has 2n parameters: n nodes and n weights. Hence we can hope to make it exact for all polynomials of degree (2n − 1) that have 2n coefficients. We are going to proof that the degree of exactness of an n-point Gaussian quadrature formula, where the nodes are the zeros of an orthogonal polynomial p_n(q) of degree n, is (2n − 1).

Theorem. Let {p_k(q)} ∀ k ∈ [0, n] be a set of orthogonal polynomials on [a, b] with respect to the inner product (1.12). Let q_j, j = 1, 2, …, n, be zeros of polynomial p_n(q). Then the quadrature rule given by eq. (1.1) has degree of exactness (2n − 1).

Proof. Given two univariate polynomials f(q) and p_n(q), the theorem of Euclidean division of polynomials (not proved here) asserts that there exist two unique polynomials t(q) and r(q) such that

f(q) = p_n(q) t(q) + r(q) and degree(r) ≤ (n − 1)

(1.22)

Let f(q) be a polynomial of degree (2n − 1). Then the quotient t(q) is a polynomial of degree (n − 1) = degree(f) − degree(p_n). Multiplying both sides of eq. (1.22) by the weighting function ω(q) and integrating, yields:

b ∫ a f(q) ω(q) dq = b ∫ a p_n(q) t(q) ω(q) dq + b ∫ a r(q) ω(q) dq = b ∫ a r(q) ω(q) dq

(1.23)

The green integral in eq. (1.23) is zero because the polynomial p_n(q) is orthogonal to all polynomials of degree ≤ (n − 1), according to eq. (1.12). Since the rule (1.18) is interpolatory, it is exact for r(q). Then

b ∫ a r(q) ω(q) dq = n ∑ i=1 w_i r(q_i) = n ∑ i=1 w_i p_n(q_i) t(q_i) + n ∑ i=1 w_i r(q_i) = n ∑ i=1 w_i [p_n(q_i) t(q_i) + r(q_i)] = n ∑ i=1 w_i f(q_i)

(1.24)

Here we have used the fact that q_i's are the zeros of p_n(q), i.e. p_n(q_i) = 0. Hence rule (1.18), which is exact for r(q), is exact also for f(q), which has degree (2n −1), i.e. I(f) = Q_n(f).

It remains to prove that the rule (1.18) is not exact for all polynomials of degree 2n. Let f(q) be a polynomial of degree 2n. Then t(q) is of degree n and <t|ω|p_n> ≠ 0. So, on one hand

b ∫ a f(q) ω(q) dq = b ∫ a p_n(q) t(q) ω(q) dq + b ∫ a r(q) ω(q) dq ≠ b ∫ a r(q) ω(q) dq

i.e. I(f) ≠ I(r) = Q_n(r). On the other hand

n ∑ i=1 w_i f(q_i) = n ∑ i=1 w_i [p_n(q_i) t(q_i) + r(q_i)] = n ∑ i=1 w_i r(q_i)

as q_i's are the zeros of p_n(q), i.e. p_n(q_i) = 0. Hence, Q_n(f) = Q_n(r) ≠ I(f) for all polynomials f of degree 2n.

1.4 - Multi-dimensional integrals. The one-dimensional quadrature rules discussed above can be directly generalized to higher dimensions. Consider the two-dimensional integral ∫∫ f(x,y) dx dy. We can integrate out one variable as follows:

∫ f(x,y) dy ≈ n_y ∑ j=1 w_y,j f(x,y_j)

(1.25)

Next we approximate the integral by the product quadrature formula

∫∫ f(x,y) dx dy ≈ n_x ∑ i=1 n_y ∑ j=1 w_x,i w_y,j f(x_i,y_j)

(1.26)

Similarly, the triple integral ∭f(x,y,z) dx dy dz can be approximated by the product quadrature rule

∫∫∫ f(x,y,z) dx dy dz ≈ n_x ∑ i=1 n_y ∑ j=1 n_z ∑ k=1 w_x,i w_y,j w_z,k f(x_i,y_j,z_k)

(1.27)

1.5 - Transformation of coordinates. Consider a mapping function f : ℝ³ → ℝ³ which takes as input the vector u ∈ ℝ³ and produces as output the vector f(u) ∈ ℝ³. (The set ℝⁿ consists of all n-tuples of real numbers and is called the “n-dimensional real space”). It is often advantageous to use other coordinates than Cartesian x, y, z system. In general, a suitable mapping function f provides transformation equations, which specify one coordinate system in terms of the other, such as (in vector notation)

r(x,y,z) =

f₁(u₁,u₂,u₃)

f₂(u₁,u₂,u₃)

f₃(u₁,u₂,u₃)

= f(u₁,u₂,u₃)

(1.28)

where x, y, z are Cartesian coordinates, and u₁, u₂, u₃ are some other coordinates. The functions f₁, f₂ and f₃ establish a one-to-one correspondence between the coordinate systems: they have to be continuous, have continuous partial derivatives and single valued inverse. So, a point r = (x,y,z) ∈ ℝ³ can also be expressed as r = (u₁,u₂,u₃), according to eq (1.28) which defines the so-called u-substitution.

Differentiating the vector function r = (x,y,z) yields the vector dr = (dx,dy,dz) = (df₁,df₂,df₃) = df, which can be written more explicitly and with matrix notation as

dr =

∂f₁ ∂u₁ du₁ + ∂f₁ ∂u₂ du₂ + ∂f₁ ∂u₃ du₃

∂f₂ ∂u₁ du₁ + ∂f₂ ∂u₂ du₂ + ∂f₂ ∂u₃ du₃

∂f₃ ∂u₁ du₁ + ∂f₃ ∂u₂ du₂ + ∂f₃ ∂u₃ du₃

= ∂ f ∂ u₁ du₁ + ∂ f ∂ u₂ du₂ + ∂ f ∂ u₃ du₃ = ∂ f ∂ u du

(1.29)

where ∂ f / ∂ u_j is a vector, whose components are the partial derivatives of x = f₁, y = f₂, and z = f₃ with respect to u_j, ∀ j = 1, 2, 3. Left-multiplying the the vector dr by its transpose yields the following equalities

dr^† dr = dr ⋅ dr = dr² = du^†( ∂ f ∂ u )† ( ∂ f ∂ u ) du = du^† J^† J du = du^† g du

(1.30)

where the Jacobian matrix J of f, also denoted by J_f and ∂(f₁,f₂,f₃) / ∂(u₁,u₂,u₃), is usually defined and arranged as follows:[N1Jacobian matrix]

J = ∂ f ∂ u = ( ∂ f ∂ u₁ ∂ f ∂ u₂ ∂ f ∂ u₃ ) =

∂f₁ / ∂u₁	∂f₁ / ∂u₂	∂f₁ / ∂u₃
∂f₂ / ∂u₁	∂f₂ / ∂u₂	∂f₂ / ∂u₃
∂f₃ / ∂u₁	∂f₃ / ∂u₂	∂f₃ / ∂u₃

(1.31)

or, component-wise: J_ij = ∂ f_i / ∂ u_j . It is worth noting that across a row of the Jacobian matrix the numerators are the same and down a column the denominators are the same. In eq (1.30) the symmetric matrix g = J^† J is called the fundamental (or metric) tensor of the Euclidean space in curvilinear coordinates. It has elements g_ii = | ∂ f / ∂ u_i |2 and g_ij = ∂ f / ∂ u_i ⋅ ∂ f / ∂ u_j for i,j = 1, 2, 3. Eq (1.30) gives the so-called first fundamental form or line element

dr² = dx² + dy² + dz²
= g₁₁ du₁² + g₂₂ du₂² + g₃₃ du₃² + 2 g₁₂ du₁ du₂ + 2 g₁₃ du₁ du₃ + 2 g₂₃ du₂ du₃

(1.32)

What is important for calculating integrals in 3D space, is the volume element dV = dx dy dz, which can be written as the absolute value of the mixed product of the three tangent vectors in eq (1.29):

dV = | ∂ f ∂ u₁ ⋅ ( ∂ f ∂ u₂ × ∂ f ∂ u₃ ) | du₁ du₂ du₃ = det( J ) du₁ du₂ du₃ = √det( g ) du₁ du₂ du₃

(1.33)

In § 2Volume Integral eq (1.33) will be used to express the Cartesian coordinates x, y, z in terms of the spherical polar coordinates r, θ, φ.

Consider now a mapping function f : ℝ → ℝ which takes as input the scalar u ∈ ℝ and produces as output the scalar f(u) ∈ ℝ. This is the case of a single variable, for which the following substitution rule holds:

b ∫ a φ(r) dr = f⁻¹(b) ∫ f⁻¹(a) φ(f(u)) f'(u) du

(1.34)

In the right hand side of eq (1.34) the variable r has been replaced by f(u), i.e. the substitution r = f(u) has been applied. f'(u) is the first derivative of f(u) with respect to u, i.e. f'(u) = df(u) / du. f⁻¹(u) is the inverse of u (not to be confused with f(u)⁻¹ that is the reciprocal of f(u): f(u)⁻¹ = 1 / f(u)).

In the following, we consider some examples of change of coordinates that allow to change the limits of integration in such a way the most appropriate rules of Gauss quadrature can be applied. Let's start with the variable transformation:

r = b − a 2 u + a + b 2 ≡ f(u)

(1.35)

From this equation:

f'(u) = df(u) du = b − a 2

(1.36)

and

f⁻¹(r) = 2r − a − b b − a ≡ u ⇒ f⁻¹(a) = − 1, f⁻¹(b) = + 1

(1.37)

so that eq (1.34) can be rewritten as:

b ∫ a φ(r) dr = +1 ∫ −1 b − a 2 φ(f(u)) du

(1.38)

An equivalent expression of eq (1.38) can be obtained by inserting the factor ω(u) ω(u)⁻¹ into the integrand of its right hand side:

b ∫ a φ(r) dr = +1 ∫ −1 b − a 2 ω(u) ω(u)⁻¹ φ(f(u)) du = +1 ∫ −1 ω(u) Φ(u) du

(1.39)

where it has been set:

Φ(u) = b − a 2 ω(u)⁻¹ φ(f(u))

(1.40)

The last integral in eq (1.39) has the proper form required by the Gauss quadrature formula:

b ∫ a φ(r) dr ≈ n ∑ i=1 w_i Φ(u_i)

(1.41)

where the u_i are either the roots of the Legendre polynomials of order n if ω(u) = 1, or the roots of the Chebyshev polynomial of the second kind if ω(u) = √1 − u², and the w_i are the associated weights. The final result is obtained by combining eqs (1.37) and (1.40) with eq (1.41):

b ∫ a φ(r) dr ≈ n ∑ i=1 v_i φ(r_i)

(1.42)

where the transformed weights, v_i, are given by

v_i = b − a 2 w_i

(1.43)

in the case of Gauss-Legendre quadrature, and

v_i = (b − a)² 4[(r − a)(b − r)]^1/2 w_i

(1.44)

in the case of Gauss-Chebyshev quadrature of the second kind.

Consider now a slightly different linear transformation, eq (1.45), and follows the same steps as before.

r = a + (b − a) u ≡ f(u)
⇓
f'(u) = b − a, f⁻¹(r) = r − a b − a ≡ u, f⁻¹(a) = 0, f⁻¹(b) = 1

(1.45)

Eqs (1.45) transform an integral over the variable r ∈ [a, b] into an integral over the new variable u ∈ [0, 1]:

b ∫ a φ(r) dr = 1 ∫ 0 (b − a) φ(f(u)) du = 1 ∫ 0 (b − a) ω(u) ω(u)⁻¹ φ(f(u)) du = 1 ∫ 0 ω(u) Φ(u) du ≈ n ∑ i=1 w_i Φ(u_i) = n ∑ i=1 v_i φ(r_i)

(1.46)

where it has been set:

Φ(u) = (b − a) ω(u)⁻¹ φ(f(u))

(1.47)

Table 1.2 suggests applying the Gauss-Gill quadrature rule to the calculation of the integral (1.46). In this case, the weight function ω(u) = ln²u is used, and yields the transformed weights:

v_i = (b − a) (ln r_i − a b − a )⁻² w_i

(1.48)

Integrals over a semi-infinite interval [r₀, ∞] are quite common in PAMoC. Among the Gauss quadratures reported in Table 1.2, only the Gauss-Laguerre rule is defined to cover the semi-infinite interval [0, ∞] and therefore it could be used without any transformation of the variable of integration. However, its useful to introduce the linear transformation (1.49),

r = r₀ + S u ≡ f(u)
⇓
f'(u) = S, f⁻¹(r) = r − r₀ S ≡ u, f⁻¹(r₀) = 0, f⁻¹(∞) = ∞

(1.49)

which leads to integration rule:

∞ ∫ r₀ φ(r) dr = ∞ ∫ 0 S φ(f(u)) du = ∞ ∫ 0 e^−u e^+u S φ(f(u)) du = ∞ ∫ 0 e^−u Φ(u) du ≈ n ∑ i=1 w_i Φ(u_i) = n ∑ i=1 v_i f(r_i)

(1.50)

where S is a scaling factor, ω(u) = e^−u is the weight function, Φ(u) = S e^+u φ(f(u)), and the transformed weights are

v_i = S exp( r_i − r₀ S ) w_i

(1.51)

2. - Volume integral

Evaluation of atomic and molecular properties requires calculation of a volume integral, which is an integral over a three dimensional domain (i.e. a region V in ℝ³) of a function f(r) = f(x,y,z) and is usually written as a triple integral:

I = ∫ V f(r) d³r = ∫ V f(r) dV = ∭ V f(x,y,z) dx dy dz

(2.1)

In the Euclidean space, the components of the position vector r are the cartesian coordinates x, y and z, and the volume element dV is given by the product of the differentials of the cartesian coordinates, dV = dx dy dz.

If function f(x,y,z) is separable along the three Cartesian coordinates, the triple integral (2.1) reduces to the product of three simple integrals, each one along a single Cartesian coordinate:

∀ f(x,y,z) = g_X(x) ⋅ g_Y(y) ⋅ g_Z(z)
⇓
∭ V f(x,y,z) dx dy dz = x₂ ∫ x₁ g_X(x) dx ⋅ y₂ ∫ y₁ g_Y(y) dy ⋅ z₂ ∫ z₁ g_Z(z) dz

(2.2)

Gaussian type orbitals (GTO's), as well as their products, are an example of functions which are separable along the three Cartesian coordinates, and the corresponding one-dimensional integrals over unbounded intervals [−∞, +∞] can be estimated by the Gauss-Hermite quadrature rule or calculated analytically.

It is often advantageous to use other coordinates than Cartesian x, y, z system. The latter are usually expressed in terms of the spherical polar coordinates r, θ, φ:

x = r cosθ sinφ, y = r sinθ sinφ, z = r cosθ

(2.5)

with r ∈ [0,∞], θ ∈ [0,π], φ ∈ [0,2π], so that the Jacobian matrix has the expression:

J(r,θ,φ) =

∂x / ∂r	∂x / ∂θ	∂x / ∂φ
∂y / ∂r	∂y / ∂θ	∂y / ∂φ
∂z / ∂r	∂z / ∂θ	∂z / ∂φ

cosθ sinφ	−r sinθ sinφ	r cosθ cosφ
sinθ sinφ	r cosθ sinφ	r sinθ sinφ
cosθ	−r sinθ	0

(2.6)

and the volume element is:

dV = r² sinθ dr dθ dφ = dr dS = r² dr dΩ

(2.7)

where we have introduced the surface element

dS = r² sinθ dθ dφ

(2.8)

spanning from θ to θ + dθ and φ to φ + dφ on a spherical surface at (constant) radius r, and the differential of the solid angle Ω = Ω(θ, φ):

dΩ = dS r² = sinθ dθ dφ

(2.9)

Then, the volume integral (2.1) can be written as a three-dimensional integral in terms of the spherical polar coordinates r, θ, and φ, or as a two-dimensional integral in terms of the radial coordinate r and the solid angle Ω:

I = +∞ ∫ 0 r² dr π ∫ 0 sinθ dθ 2π ∫ 0 f(r,θ,φ) dφ = +∞ ∫ 0 r² dr ∫ Ω f(r,Ω) dΩ

(2.10)

It can be calculated by the one-dimensional radial integration:

I = +∞ ∫ 0 r² g(r) dr

(2.11)

of a function g(r), which provides the spherical average of f(x, y, z) through the evaluation of a two-dimensional surface integral over the unit sphere at (constant) radius r:

g(r) = π ∫ 0 sinθ dθ 2π ∫ 0 f(r,θ,φ) dφ = ∫ Ω f(r,Ω) dΩ

(2.12)

The integral is numerically approximated as a sum of weighted function values, sampled over a given set of points c_i = r_i, θ_i, φ_i, Ω_i:

∫ V f(r) dV ≈ N_r ∑ i=1 w_r,i N_θ ∑ j=1 w_θ,j N_φ ∑ k=1 w_φ,k f(r_i,θ_j,φ_k) ≈ N_r ∑ i=1 w_r,i N_Ω ∑ j=1 w_Ω,j f(r_i,Ω_j)

(2.13)

2.1. - Partitioning into atomic subintegrals.

In a molecule, the density ρ(r) has cusps at the positions of the nuclei, so that a simple cartesian grid for the entire molecule cannot account properly for the accumulation of density at that positions. Then, following design principles put forward by Becke in 1988, the molecular integration is broken up into separate, but overlapping atomic contributions.[2Becke, A. D.
J. Chem. Phys. 1988, 88, 2547-2553.] These single-center atomic subintegrals are then computed on atomic grids. Finally, the results are summed together to give the molecular integral (2.1).
Different partitioning schemes are available in PAMoC for experimental and/or theoretical densities:

2.2. - Angular integral.

The great simplicity of the three-terms product formula (N_r, N_θ, N_φ), eq. (2.13), which separates the integral into three one-dimensional quadratures over the coordinates r, θ, and φ, has led Murray, Handy and Laming in 1993 to recommend it.[3Murray, C. W.; Handy, N. C.; Laming, G. J.
Mol. Phys. 1993, 78, 997-1014.] In this case, a standard choice for integration of the angular part is a spherical product formula which uses the trapezoidal rule along φ direction and Gauss-Legendre quadrature along θ direction. Usually, the angular grid is characterized by a single integer L, which describes the maximum degree of spherical harmonic which may be integrated exactly; this implies N_φ = L + 1 equally spaced points in φ space and N_θ = (L + 1)/2 Gauss-Legendre points in θ space, for a total of N_θ⋅N_φ = (L + 1)²/2 angular quadrature points. This quadrature rule is still available in PAMoC for historical reasons, since it was used in some old codes from which PAMoC evolved.

There are highly efficient algorithms for numerically integrating on the surface of a sphere that clearly outperform the alternative integration over the individual angular coordinates. Indeed, Becke in 1988[2Becke, A. D.
J. Chem. Phys. 1988, 88, 2547-2553.] and Gill, Johnson and Pople (GJP) in 1993[4Gill, P. M. W.; Johnson, B. G.; Pople, J. A.
Chem. Phys. Lett. 1993, 209, 506-512.] found that a two-terms product formula (N_r, N_Ω), which separates the integral (2.13) into two one-dimensional quadratures on the radial coordinate r and the angular coordinate Ω is more efficient than separating also the two angular integrations on θ and φ. Since then, the general consensus seems to have focused on the so-called two-dimensional Lebedev grids,[5(a) Lebedev, V.I.
USSR Comp. Math. and Math. Phys. 1975, 15(1), 44-51. Zh. vychisl. Mat. mat. Fiz. 1975, 15(1), 48-54.
(b) Lebedev, V.I.
USSR Comp. Math. and Math. Phys. 1976, 16(2), 10-24. Zh. vychisl. Mat. mat. Fiz. 1976, 16(2), 293-306.
(c) Lebedev, V.I.
Siberian. Math. J. 1977, 18(1), 99-107. Sibirskii Matematicheskii Zhurnal 1977, 18(1), 132-142.
(d) Lebedev, V. I.; Skorokhodov, A. L.
Russian Acad. Sci. Dokl. Math. 1992, 45, 587-592.
(e) Lebedev, V. I.
Russian Acad. Sci. Dokl. Math. 1995, 50, 283-286.
(f) Lebedev, V.I.; Laikov, D.N.
Dokl. Math. 1999, 59, 477-481.] which are the PAMoC method of choice to evaluate the spherical integral of Eq. (2.12). Each of Lebedev grids are characterized by the fixed number of angular quadrature points N_Ω ≈ (L + 1)²/3, which exactly integrate the spherical harmonics having up to a maximum degree L.

2.3. - Radial integral and transformations of the radial coordinate.

The general methodology to calculate the integral (2.11) is to map the interval [0, ∞] to a finite interval [a, b] of the variable q by a suitable variable transformation r = r(q) ⇒ dr = r'(q) dq, and then to use a quadrature formula defined on this interval. The integral (2.11) takes then the form

+∞ ∫ 0 r² g(r) dr = b ∫ a ω(q) ω⁻¹(q) r²(q) r'(q) g[r(q)] dq = b ∫ a ω(q) G(q) dq
≈ n ∑ i=1 w_i G(q_i) = n ∑ i=1 w_i ω⁻¹(q_i) r²(q_i) r'(q_i) g[r(q_i)] = n ∑ i=1 v_i g(q_i)

(2.14)

where we have set G(q) = ω⁻¹(q) r²(q) r'(q) g[r(q)] and v_i = w_i ω⁻¹(q_i) r²(q_i) r'(q_i) . The choice of the mapping is crucial. The mapping determines how the radial points are distributed in the molecular space and if the core and the chemical bonding regions are appropriately represented in the integration. The function r(q) has to be chosen in a way that a high resolution is provided in the core and, to a lesser extent, in the valence region of the atom to ensure an accurate integration but sparse outside the atomic region to allow an economical calculation. The resolution is controlled by the value of the derivative r'(q): a small value of r'(q) indicates that a given interval for r is mapped onto a large interval of q, which implies a high resolution; consequently, a large value of r'(q) implies a low resolution. In summary, r'(q) should be small where r(q) is small and large where r(q) is large.

Since it is hard to define the detailed prescriptions a mapping function should obey, in order for the radial quadrature to be efficient, many different mapping schemes have been introduced in literature so far.[2Becke, A. D.
J. Chem. Phys. 1988, 88, 2547-2553.; 3Murray, C. W.; Handy, N. C.; Laming, G. J.
Mol. Phys. 1993, 78, 997-1014.; 4Gill, P. M. W.; Johnson, B. G.; Pople, J. A.
Chem. Phys. Lett. 1993, 209, 506-512.; 6Gill, P.M.W.; Johnson, B.J.; Pople, J.A.; Frisch, M.J.
Intern. J. Quantum Chem. Symp. 1992, 26, 319-331.; 7Treutler, O.; Ahlrichs, R.
J. Chem. Phys. 1995, 102, 346-354.; 8Mura, M. E.; Knowles, P. J.
J. Chem. Phys. 1996, 104, 9848-9858.; 9Lindh, R.; Malmqvist, P.-A.; Gagliardi, L.
Theor. Chem. Acc. 2001, 106, 178.; 10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003,24, 732-740.] Finding a mapping function consists in transforming the integral by transition to another variable of integration. Such a procedure is one of the methods for calculating an integral in one real variable, which is known as integration by substitution.

The transformed coordinate q_i can be sampled over a set of equally spaced points and used in combinations with extended forms of Newton-Cotes quadrature formulas (cf Table 1.1). On the other hand, the evaluation points q_i can be chosen as the roots of a polynomial which is orthogonal in the same interval of the variable q with respect to a weighting function ω(q). A representative set of these orthogonal polynomials is given in Table 1.2.

A number of different mappings of the radial coordinate r, defined over the semi-infinite interval [r₀, ∞] or the finite interval [r₀, r_max], onto a new coordinate q, defined over the interval [a, b] with values chosen as either equispaced points or roots of polynomials orthogonal in the same interval [a, b], is listed in Table 2.1. Additional information can be found in Sections 3−8 and 10.

**Table 2.1** − Mappings of the radial coordinate r, defined over the interval [r₀, *r_max*], onto a new coordinate q, whose values are chosen as either equispaced points or roots of polynomials orthogonal in the interval [a, b]. The option values of the associated quadrature rules are also given.
{r_i}	grid	r_i − r₀	q_i	{q_i}	`radrule`
[r₀, ∞]	MultiExp	− R ln q_i	exp [−(r_i − r₀)/R]	[0, 1]	31, 71
[r₀, ∞]	Knowles	− R ln (1 − q_i^k)	^{^k}√1 − exp [−(r_i − r₀)/R]	[0, 1]	32, 72
[r₀, ∞]	Handy	R q_i^m / (1 − q_i)^m	^{^m}√r_i − r₀ / ^{^m}√R − ^{^m}√r_i − r₀	[0, 1]	33, 73
[r₀, r_max]	Handy	(r_max − r₀) q_i^m / 1 + (r_max − r₀ − 2^m)(1 − q_i)^m	m√ (r_i − r₀) (r_max − r₀ − 2^m + 1) / (r_i − r₀)(r_max − r₀ − 2^m) + r_max − r₀	[0, 1]	34, 74
[r₀, ∞]	Becke	R 1 + q_i / 1 − q_i	r_i − r₀ − R / r_i − r₀ + R	[−1, +1]	15, 25, 75
[r₀, ∞]	Ahlrichs	− R (1 + q_i)^α / ln 2 ln 1 − q_i / 2		[−1, +1]	16, 26, 76
[r₀, r_max]	linear	r_max − r₀ / 2(1 + q_i)	2 r_i − (r_max + r₀) / r_max − r₀	[−1, +1]	17, 27, 77
[r₀, r_max]	linear	(r_max − r₀) q_i	r_i − r₀ / r_max − r₀	[0, 1]	37, 77
[r₀, ∞]	linear	R q_i	r_i − r₀ / R	[0, ∞]	47, 57, 77

2.3.4. - Standardization of quadrature grids. In order to compare the roots and weights from the various quadrature schemes, Gill and Chien[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.] chose the R values so that the middle point of each quadrature is unity, i.e. r(q_k) − r₀ = 1 for k = (n+1)/2. They called the resulting values the standardized roots and weights, and the standardizing factor was defined as:

R = 1 r[q_(n+1)/2] − r₀

(2.15)

However, such a definition makes R dependent on n and is ambigous when n is even. For this reason, and in a more general way, PAMoC uses a standardization factor σ, which is defined in terms of the value of the coordinate q at the center of the interval spanned by the variable q itself:

σ = 1 r(q_center) − r₀

(2.16)

As a consequence, the standardizing factor, σ, depends only on the type of transformation, and not on how the points q_i are chosen nor on their number n. In addition, PAMoC defines R as the product of σ and the parameter R_cov, which eventually can be used to adjust the grid to fit different atomic shapes:

R = σ R_cov

(2.17)

Typically, R_cov is chosen as the covalent radius of the atom (see next section).

As shown in Table 2.1, MultiExp, Knowles, and Handy transformations map the radial coordinate r ∈ [r₀, ∞] into the finite interval [0, 1], whose midpoint is q_center = ¹⁄₂. Among the qudrature rules available in PAMoC, the Gauss-Gill and the extended trapezoidal rules have roots in the range [0, 1], and therefore can be used in combination with the MultiExp, Knowles and Handy grids, which are standardized by the following factors:

σ_MutiExp = − 1 / ln q_center = 1 / ln 2 = 1.442695
σ_Knowles = − 1 / ln (1 − q^k_center) (e.g.: σ_Log1 = 1.442695 and σ_Log3 = 7.488876)
σ_Handy = ( 1 − q_center / q_center)^m = 1

Becke and Ahlrichs transformations map the radial coordinate into the finite interval [−1, +1], whose midpoint is q_center = 0 and the standardization factor is σ_Becke = σ_Ahlrichs = 1. The roots of Legendre and Chebyshev polynomials fall in the same interval, occur symmetrically about the origin and include the origin itself, so that combining the Gauss-Legendre and Gauss-Chebyshev quadratures with Becke and Ahlrichs transformations yield grids a which are standardized implicitly.

The Laguerre grid spans a semi-infinite interval for which q_center cannot be defined. Therefore its standardizing factor is calculated by eq. (2.15) and depends on the value of the middle root and n:

σ_Laguerre = 1 q_(n+1)/2

2.4. - Scale factor of radial quadrature points: the atomic radius. The nodes of the quadrature rules are proportional to arbitrary scale factors R (not necessarily the same) and the corresponding weights are proportional to R³. The value of this parameter corresponds to the midpoint of the integration interval at q = 0. The parameter R is an atomic radius which measures the radial extent of the atom in question. In Becke's grid R is chosen as half of the Bragg-Slater radius[16Bragg, W. L.
Philos. Mag. 1920, 40, 169-189., 17Slater, J. C.
J. Chem. Phys. 1964, 41, 3199-3204.] of the respective atom, except for hydrogen in which case the factor 1/2 is not applied. Original values of Bragg-Slater radii[17Slater, J. C.
J. Chem. Phys. 1964, 41, 3199-3204.] are reported in Table 2.2. Revisited values[18Cordero, B.; Gómez, V.; Platero-Prats, A. E.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S.
Dalton Trans. 2008, 2832-2838.] are given in Table 2.3.

**Table 2.2** − Bragg-Slater empirically measured covalent radii for the elements (Ångstroms).[17Slater, J. C.
*J. Chem. Phys.* **1964**, 41, 3199-3204.]
H																	He
0.25
Li	Be											B	C	N	O	F	Ne
1.45	1.05											0.85	0.70	0.65	0.60	0.50
Na	Mg											Al	Si	P	S	Cl	Ar
1.80	1.50											1.25	1.10	1.00	1.00	1.00
K	Ca	Sc	Ti	V	Cr	Mn	Fe	Co	Ni	Cu	Zn	Ga	Ge	As	Se	Br	Kr
2.20	1.80	1.60	1.40	1.35	1.40	1.40	1.40	1.35	1.35	1.35	1.35	1.30	1.25	1.15	1.15	1.15
Rb	Sr	Y	Zr	Nb	Mo	Tc	Ru	Rh	Pd	Ag	Cd	In	Sn	Sb	Te	I	Xe
2.35	2.00	1.80	1.55	1.45	1.45	1.35	1.30	1.35	1.40	1.60	1.55	1.55	1.45	1.45	1.40	1.40
Cs	Ba	La	Hf	Ta	W	Re	Os	Ir	Pt	Au	Hg	Tl	Pb	Bi	Po	At	Rn
2.60	2.15	1.95	1.55	1.45	1.35	1.35	1.30	1.35	1.35	1.35	1.50	1.90	1.80	1.60	1.90
		↓
		Ce	Pr	Nd	Pm	Sm	Eu	Gd	Tb	Dy	Ho	Er	Tm	Yb	Lu
		1.85	1.85	1.85	1.85	1.85	1.85	1.80	1.75	1.75	1.75	1.75	1.75	1.75	1.75

**Table 2.3** − Covalent radii (Ångstroms), from analysis of the Cambridge Structural Database.[18Cordero, B.; Gómez, V.; Platero-Prats, A. E.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S.
*Dalton Trans.* **2008**, 2832-2838.]
H																	He
0.31																	0.28
Li	Be											B	C	N	O	F	Ne
1.28	0.96											0.84	0.76	0.71	0.66	0.57	0.58
Na	Mg											Al	Si	P	S	Cl	Ar
1.66	1.41											1.21	1.11	1.07	1.05	1.02	1.06
K	Ca	Sc	Ti	V	Cr	Mn	Fe	Co	Ni	Cu	Zn	Ga	Ge	As	Se	Br	Kr
2.03	1.76	1.70	1.60	1.53	1.39	1.39	1.32	1.26	1.24	1.32	1.22	1.22	1.20	1.19	1.20	1.20	1.16
Rb	Sr	Y	Zr	Nb	Mo	Tc	Ru	Rh	Pd	Ag	Cd	In	Sn	Sb	Te	I	Xe
2.20	1.95	1.90	1.75	1.64	1.54	1.47	1.46	1.42	1.39	1.45	1.44	1.42	1.39	1.39	1.38	1.39	1.40
Cs	Ba	La	Hf	Ta	W	Re	Os	Ir	Pt	Au	Hg	Tl	Pb	Bi	Po	At	Rn
2.44	2.15	2.07	1.75	1.70	1.62	1.51	1.44	1.41	1.36	1.36	1.32	1.45	1.46	1.48	1.40	1.50	1.50
		↓
		Ce	Pr	Nd	Pm	Sm	Eu	Gd	Tb	Dy	Ho	Er	Tm	Yb	Lu
		2.04	2.03	2.01	1.99	1.98	1.98	1.96	1.94	1.92	1.92	1.89	1.90	1.87	1.87

In the so-called SG-1 grid by GJP,[4Gill, P. M. W.; Johnson, B. G.; Pople, J. A.
Chem. Phys. Lett. 1993, 209, 506-512.] the parameter R was chosen as the abscissa of the maximum of the radial probability function 4 πr²χ²(r) of the valence atomic orbital χ(r) given by Slater's well known rules.[19Slater, J. C.
Phys. Rev. 1930, 36, 57-64.] The atomic radii which follow from this definition are given in Table 2.4 for the atoms H to Ar. The atomic radii for the atoms K to Rn are those determined by Clementi[20Clementi, E.; Raimondi, D. L.; Reinhardt, W. P.
J. Chem. Phys. 1967, 47, 1300-1307.] from minimal-basis-set SCF functions and reported in Table 2.5. The atomic radii reported in Tables 2.2 - 2.5 are compared in Figure 2.1.

**Table 2.4** − Atomic radii (bohr), corresponding to the maximum of the radial probability function of the valence atomic orbital.[4Gill, P. M. W.; Johnson, B. G.; Pople, J. A.
*Chem. Phys. Lett.* **1993**, *209*, 506-512.]
H							He
1.0000							0.5882
Li	Be	B	C	N	O	F	Ne
3.0769	2.0513	1.5385	1.2308	1.0256	0.8791	0.7692	0.6838
Na	Mg	Al	Si	P	S	Cl	Ar
4.0909	3.1579	2.5714	2.1687	1.8750	1.6514	1.4754	1.3333

**Table 2.5** − Atomic radii (Ångstroms), determined from minimal-basis-set SCF functions.[20Clementi, E.; Raimondi, D. L.; Reinhardt, W. P.
*J. Chem. Phys.* **1967**, 47, 1300-1307.]
H																	He
a₀																	0.31
Li	Be											B	C	N	O	F	Ne
1.67	1.12											0.87	0.67	0.56	0.48	0.42	0.38
Na	Mg											Al	Si	P	S	Cl	Ar
1.90	1.45											1.18	1.11	0.98	0.88	0.79	0.71
K	Ca	Sc	Ti	V	Cr	Mn	Fe	Co	Ni	Cu	Zn	Ga	Ge	As	Se	Br	Kr
2.43	1.94	1.84	1.76	1.71	1.66	1.61	1.56	1.52	1.49	1.45	1.42	1.36	1.25	1.14	1.63	0.94	0.88
Rb	Sr	Y	Zr	Nb	Mo	Tc	Ru	Rh	Pd	Ag	Cd	In	Sn	Sb	Te	I	Xe
2.65	2.19	2.12	2.06	1.98	1.90	1.83	1.78	1.73	1.69	1.65	1.61	1.56	1.45	1.33	1.23	1.15	1.08
Cs	Ba	La	Hf	Ta	W	Re	Os	Ir	Pt	Au	Hg	Tl	Pb	Bi	Po	At	Rn
2.98	2.53	2.50	2.08	2.00	1.93	1.88	1.85	1.80	1.77	1.74	1.71	1.56	1.54	1.43	1.35	1.27	1.20
		↓
		Ce	Pr	Nd	Pm	Sm	Eu	Gd	Tb	Dy	Ho	Er	Tm	Yb	Lu
		2.50	2.08	2.00	1.93	1.88	1.85	1.80	1.77	1.74	1.71	1.56	1.54	1.43	1.35

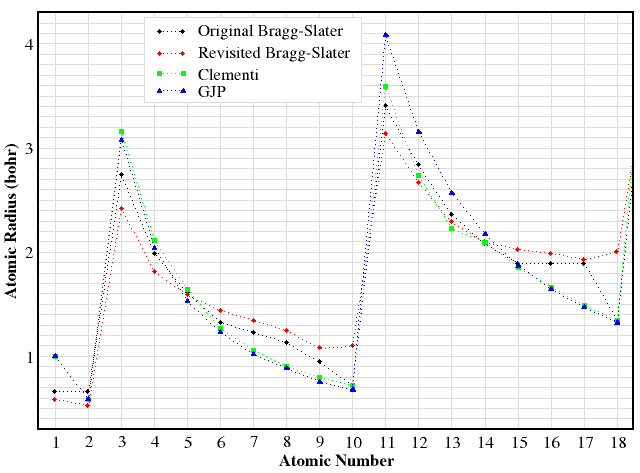Figure 2.1: Covalent radius (bohr) as a function of the atomic number: (a) on mouse out, for atoms H to Ar, (b) on mouse over, for atoms H to Cm.

**Table 2.6** − Partitioning parameters used in the pruned Lebedev (*N_r*,*N_Ω*) and spherical product (*N_r*,*N_θ*,*N_φ*) grids.
Size of atomic regions
Atom		α₁	α₂	α₃	α₄	outer region
H-He		0.2500	0.5000	1.0000	4.5000
Li-Ne		0.1667	0.5000	0.9000	3.5000
Na-Ar		0.1000	0.4000	0.8000	2.5000
K-Kr		0.0200	0.1000	0.2000	3.5000
Lebedev grid
(N_r,N_Ω)	L	α₁	α₂	α₃	α₄	outer region
(50,194)	23	6	38	86	194	86
(75,302)	29	26	86	146	302	146
(99,590)	41	86	194	302	590	302
(110,770)	47	110	230	350	770	350
(150,974)	53	146	266	434	974	434
(185,1202)	59	170	350	590	1202	590
(225,5720)	131	434	590	1202	5720	1202
Spherical product grid
(N_r,N_θ,N_φ)	L	α₁	α₂	α₃	α₄	outer region
(50,15,30)	29	50	128	200	450	200
(75,25,50)	49	128	200	450	1250	450
(99,48,96)	95	200	450	1250	4608	1250

2.5. - Grid pruning. In order to cut down the number of grid points and hence to increase the efficiency of the numerical integration, a technique called grid pruning is frequently used. The underlying idea is that as one approaches the nucleus, the electron density loses more and more its angular structure and becomes increasingly spherically symmetric. Hence, for spheres at small distances from the nucleus a progressively smaller amount of angular grid points should suffice. Similar arguments apply if we analyze the situation at large values of r. Here, the actual magnitude of ρ(r) becomes so small that again we can get away with much less sophisticated angular grids without loosing any significant accuracy. In a pruned grid one exploits these observations and the space around each atom is partitioned into various regions. Within these regions, whose sizes of course depend on the actual atom, Lebedev grids of varying density are used. Close to the nucleus fairly coarse grids are sufficient, while dense ones are employed at intermediate distances and again coarser grids as we move farther away from the nucleus. This technique is used in most modern density functional programs.

For example, in 1993 Gill, Johnson and Pople proposed that the quadrature grids obtained by the combination of the N_r-point Euler-Maclaurin radial grid and the N_Ω-point Lebedev angular grid, viz. EML(N_r,N_Ω), or the N_θ×N_φ-point spherical product grid, viz. EMSP(N_r,N_θ,N_φ) could be reduced in size, while maintaining their effectiveness, by allowing the number of points N_Ω or N_θ×N_φ to become dependent on r, so that different angular grids can be used on different concentric spheres.[4Gill, P. M. W.; Johnson, B. G.; Pople, J. A.
Chem. Phys. Lett. 1993, 209, 506-512.] Given four numbers {α₁, α₂, α₃, α₄} and an atomic radius R, the four spheres of radius α₁R, α₂R, α₃R, and α₄R obviously partition an atom into five regions. The size of each region depends on the central atom. The angular grids used in these regions, together with the appropriate α-parameters determined for the atoms H to Kr, are given in Table 2.6. The so-called standard grid SG-1 was designed to give numerical integration errors of about 0.2 kcal mol⁻¹ for medium sized molecules, while using as few grid points as possible. The grid is derived from the EML(50,194) grid, which has 50 radial points, given by the Euler-Maclaurin rules, and 194 angular points positioned by the Lebedev rules. The SG-1 grid partitions space into five spherical regions around the atom and then uses Lebedev grids with 6, 38, 86, 194 and 86 points respectively. This produces about 2500 points per atom, roughly a quarter the size of the EML(50,194) grid, yet yielding similar (within a few μ-Hartree) accuracy. Similarly, the fairly dense integration mesh EML(75,302) contains 75 radial shells and 302 angular points per shell. Due to the pruning the actual number of integration points per atom is reduced to only around 7000, just a third of the regular size of 75 × 302 = 22650 points.

**Table 2.7** − Lebedev partition, number *N_r* of radial points, scale factor R and total number N_tot of grid points in the SG-0 grid (from ref 26Chien, S.-H.; Gill, P. M. W.;
*J. Comput. Chem.* **2006**, 27, 730-739.).
Element	Lebedev partition	N_r	R	N_tot
H	6⁶ 18³ 26¹ 38¹ 74¹ 110¹ 146⁶ 86¹ 50¹ 38¹ 18¹	23	1.30	1406
Li	6⁶ 18³ 26¹ 38¹ 74¹ 110¹ 146⁶ 86¹ 50¹ 38¹ 18¹	23	1.95	1406
Be	6⁴ 18² 26¹ 38² 74¹ 86¹ 110² 146⁵ 50¹ 38¹ 18¹ 6²	23	2.20	1390
B	6⁴ 26⁴ 38³ 86³ 146⁶ 38¹ 6²	23	1.45	1426
C	6⁶ 18² 26¹ 38² 50² 86¹ 110¹ 146¹ 170² 146² 86¹ 38¹ 18¹	23	1.20	1390
N	6⁶ 18³ 26¹ 38² 74² 110¹ 170² 146³ 86¹ 50²	23	1.10	1414
O	6⁵ 18¹ 26² 38¹ 50⁴ 86¹ 110⁵ 86¹ 50¹ 38¹ 6¹	23	1.10	1154
F	6⁴ 38² 50⁴ 74² 110² 146² 110² 86³ 50¹ 6¹	23	1.20	1494
Na	6⁶ 18² 26³ 38¹ 50² 110⁸ 74² 6²	26	2.30	1328
Mg	6⁵ 18² 26² 38² 50² 74¹ 110² 146⁴ 110¹ 86¹ 38² 18¹ 6¹	26	2.20	1492
Al	6⁶ 18² 26¹ 38² 50² 74¹ 86¹ 146² 170² 110² 86¹ 74¹ 26¹ 18¹ 6¹	26	2.10	1496
Si	6⁵ 18⁴ 38⁴ 50³ 74¹ 110² 146¹ 170³ 86¹ 50¹ 6¹	26	1.30	1496
P	6⁵ 18⁴ 38⁴ 50³ 74¹ 110² 146¹ 170³ 86¹ 50¹ 6¹	26	1.30	1496
S	6⁴ 18¹ 26⁸ 38² 50¹ 74² 110¹ 170³ 146¹ 110¹ 50¹ 6¹	26	1.10	1456
Cl	6⁴ 18⁷ 26² 38² 50¹ 74¹ 110² 170³ 146¹ 110¹ 86¹ 6¹	26	1.45	1480

More recently, in 2006 Chien and Gill reported "the development of a new standard quadrature grid, SG-0, designed to be approximately half as large as, and to provide approximately half the accuracy of, the established SG-1 grid".[26Chien, S.-H.; Gill, P. M. W.
J. Comput. Chem. 2006, 27, 730-739.] It is based on MultiExp[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.] and Lebedev quadrature for radial and angular coordinates, respectively, and can be referred to as MEL(23,170) for first-row atoms and MEL(26,170) for the second row elements. The pruning process is more highly resolved in SG-0 than in SG-1. "The SG-0 grid for each of the first- and second-row elements studied is given in Table 2.7. Each grid is defined by the number N_r of radial grid points, the radial scale factor R, and the number of angular grid points at each of the radial points. The total number N_tot of grid points on each atom is also listed. The SG-0 grid for any element not listed in Table 2.7 is defined to be the same as the SG-1 grid for that element. In the second column of Table 2.7, the notation x^y indicates that the x-point Lebedev grid is used at y successive radial points. For example, the SG-0 grid for the hydrogen atom has 23 radial points and the configuration 6⁶, 18³, 26¹, 38¹, 74¹, 110¹, 146⁶, 86¹, 50¹, 38¹, 18¹ indicates that a six-point Lebedev angular grid is used at each of the six innermost radial points, an 18-point angular grid at each of the next three radial points, followed by a single 26-point grid, a single 38-point grid, and so forth."

3. Lebedev angular quadrature

This section briefly discusses the evaluation of the angular integral (2.12) using Lebedev quadrature:

g(r) = π ∫ 0 sinθ dθ 2π ∫ 0 f(r,θ,φ) dφ = ∫ Ω f(r,Ω) dΩ ≈ n ∑ i=1 w_i f(r, Ω_i) = n ∑ i=1 w_i f(r, θ_i, φ_i)

(9.1)

**Table 9.1** − Degree L and points *N_Ω* ≈ (L + 1)² / 3 of Lebedev rules.
L	N_Ω	L	N_Ω	L	N_Ω	L	N_Ω
3	6	19	146	41	590	89	2702
5	14	21	170	47	770	95	3074
7	26	23	194	53	974	101	3470
9	38	25	230	59	1202	107	3890
11	50	27	266	65	1454	113	4334
13	74	29	302	71	1730	119	4802
15	86	31	350	77	2030	125	5294
17	110	35	434	83	2354	131	5810

where the particular grid points (θ_i, φ_i, or Ω_i) and grid weights, w_i, are to be determined. It's worth recalling that the angular coordinate Ω is related to cartesian coordinates r ≡ {x, y, z}, via Ω = r / |r|. In other words, Ω represents the Cartesian coordinates of a vector pointing to the surface of a unit sphere. Angular integration, therefore, is the integration of a function living on the surface of a unit sphere (centered at a constant point r). The orthogonal (with respect to the weight function ω(Ω) = 1) polynomials living on the surface of a unit sphere are special functions called spherical harmonics. A set of quadrature weights and roots for spherical harmonics could be obtained by the usual procedure to generate Gauss quadrature formulas.[24 Anderson, D.G.
Math. Comp. 1965, 19, 477-481.; 25Golub, G.H.; Welsch, J.H.
Math. Comp. 1969, 23, 221-230.] For an ideal formula, the integration points should obviously be distributed over the surface of the sphere as uniformly as possible. A perfectly uniform distribution is provided by the vertices or the face centroids of a regular polyhedron. Lebedev and Laikov developed a highly efficient set of quadrature points which are invariant under the octahedral rotation group with inversion. The resulting sets of weights and points are referred to as Lebedev angular quadrature grids and are generally regarded as being superior (number of points vs. accuracy) to other angular quadrature schemes.[5(a) Lebedev, V.I.
USSR Comp. Math. and Math. Phys. 1975, 15(1), 44-51. Zh. vychisl. Mat. mat. Fiz. 1975, 15(1), 48-54.
(b) Lebedev, V.I.
USSR Comp. Math. and Math. Phys. 1976, 16(2), 10-24. Zh. vychisl. Mat. mat. Fiz. 1976, 16(2), 293-306.
(c) Lebedev, V.I.
Siberian. Math. J. 1977, 18(1), 99-107. Sibirskii Matematicheskii Zhurnal 1977, 18(1), 132-142.
(d) Lebedev, V. I.; Skorokhodov, A. L.
Russian Acad. Sci. Dokl. Math. 1992, 45, 587-592.
(e) Lebedev, V. I.
Russian Acad. Sci. Dokl. Math. 1995, 50, 283-286.
(f) Lebedev, V.I.; Laikov, D.N.
Dokl. Math. 1999, 59, 477-481.] Each of Lebedev grids are characterized by the fixed number of angular quadrature points N_Ω ≈ (L + 1)²/3, which exactly integrate the spherical harmonics having up to a maximum degree L. The sets of fixed sizes, called rules, which are available in PAMoC, are listed in Table 9.1. The corresponding code is distributed through CCL (fortran source).

3. Gauss-Legendre quadrature

Gauss-Legendre quadrature provides an approximate solution to the definite integral of a function f(q) over the interval [−1, 1] as a weighted sum of function values at specified points within the domain of integration:

+1 ∫ −1 f(q) dq ≈ n ∑ i=1 w_i f(q_i)

(3.1)

A n-point quadrature rule as above will only produce accurate results if the function f(q) is well approximated by a polynomial function within the range [−1, 1]. It is constructed to yield an exact result for polynomials of degree (2n − 1) or less, by a suitable choice of the points q_i and weights w_i for i = 1, ..., n. The evaluation points q_i for quadrature order n are just the roots of the Legendre polynomials P_n(q), which occur symmetrically about 0. In other words, with the n-th polynomial normalized to give P_n(1) = 1, the i-th node, q_i, is the i-th root of P_n, with associated weight w_i.

**Table 3.1** − First six Legendre polynomials with associated roots and weights.
P_n(q) = 1 / 2ⁿ ⌊n/2⌋ ∑ k=0 (−1)^k (2n − 2k)! / k! (n − k)! (n − 2k)! q^n−2k	q_i	w_i = 2 / (1 − q_i²) [P'_n(q_i)]²
P₀(q) = 1
P₁(q) = q	q₁ = 0	w₁ = 2
P₂(q) = (3q² − 1)/2	q_1,2 = ∓√⅓ = ∓0.577350	w_1,2 = 1
P₃(q) = (5q³ − 3q)/2	q_1,3 = ∓√⅗ = ∓0.774597	w_1,3 = ⁵⁄₉ = 0.555556
P₃(q) = (5q³ − 3q)/2	q₂ = 0	w₂ = ⁸⁄₉ = 0.888889
P₄(q) = (35q⁴ − 30q² + 3)/8	q_1,4 = ∓√³⁄₇ + ²⁄₇√⁶⁄₅ = ∓0.861136	w_1,4 = (18 − √30)/36 = 0.347855
P₄(q) = (35q⁴ − 30q² + 3)/8	q_2,3 = ∓√³⁄₇ − ²⁄₇√⁶⁄₅ = ∓0.339981	w_2,3 = (18 + √30)/36 = 0.652145
P₅(q) = (63q⁵ − 70q³ + 15q)/8	q_1,5 = ∓⅓√5 + 2√¹⁰⁄₇ = ∓0.906180	w_1,5 = (322 − 13√70)/900 = 0.236927
	q_2,4 = ∓⅓√5 − 2√¹⁰⁄₇ = ∓0.538469	w_2,4 = (322 + 13√70)/900 = 0.478629
	q₃ = 0	w₃ = 128/225 = 0.568889
P₆(q) = (231q⁶ − 315q⁴ + 105q² − 5)/16	q_1,6 = ∓0.932470	w_1,6 = 0.171324
	q_2,5 = ∓0.661209	w_2,5 = 0.360762
	q_3,4 = ∓0.238619	w_3,4 = 0.467914
The floor function ⌊n/2⌋ specifies the largest integer less than or equal to n/2.

The integral of a function f(r) over the interval [a, b] can still be evaluated by the Gauss-Legendre formula, after a suitable variable substitution like the following:

r = b − a 2 q + a + b 2 ≡ r(q) ⇒ dr = b − a 2 dq

(3.2)

which changes the integral over [a, b] into an integral over [-1, 1] in the following way:

b ∫ a f(r) dr = +1 ∫ −1 b − a 2 f(r) dq ≈ n ∑ i=1 b − a 2 w_i f(r_i) = n ∑ i=1 ν_i f(r_i)

(3.3)

where n is the number of quadrature points used, the q_i are the roots of the Legendre polynomial P_n(q) with associated weights w_i, and the ν_i = b − a / 2 w_i are the transformed weights.

The following paragraphs describe two main applications of the Gauss-Legendre quadrature rule in PAMoC.

theta quadrature over the interval [0, π]. In the case of explicit user request to estimate the angular integral of eq. (2.12) by the two-term (N_θ, N_φ) product formula ("intgrid 8 | 9 | 10" and "intgrid -mmmlll"), PAMoC employes the Gauss-Legendre formula for the theta quadrature over the interval [0, π]. To this aim, the variable substitution

q = cosθ ⇒ dq = − sinθ dθ

(3.4)

changes the integral over θ ∈ [0, π] into an integral over q ∈ [−1, 1] in the following way

π ∫ 0 f(θ) sinθ dθ = − −1 ∫ 1 f(q) dq = 1 ∫ −1 f(q) dq ≈ n ∑ j=1 w_j f(q_j)

(3.5)

Radial integral. The Gauss-Legendre quadrature rule can also be used by PAMoC to estimate the radial integral (2.11), in conjunction with a suitable variable transformation to map the semi-infinite interval spanned by the radial coordinate r into the finite interval [−1, +1] of the variable q. This is accomplished by two transformations of the radial coordinate, due to Becke[2Becke, A. D.
J. Chem. Phys. 1988, 88, 2547-2553.] and Ahlrichs,[7Treutler, O.; Ahlrichs, R.
J. Chem. Phys. 1995, 102, 346-354.] which are described in section 7 with more details. In addition, the linear transformation (3.2) is also available. The appropriate weights for the Gauss-Legendre quadrature are given by eqs. (3.6), (3.7), and (3.8), respectively,

Becke: ν_i = 2 / 1 − q_i² (r_i − r₀) r_i² w_i	(3.6)
Ahlrichs: ν_i = (r_i − r₀) r_i² ( α / 1 + q_i − 1 / 1 − q_i ln⁻¹ 1 − q_i / 2) w_i	(3.7)
Linear: ν_i = b − a / 2 r_i² w_i	(3.8)

where q_i and w_i are roots and weights of the Gauss-Legendre quadrature rule, and r_i is defined by eqs. (8.4), (8.8), and (3.2), respectively.

The n-point Gauss-Legendre quadrature rule integrates exactly all spherical harmonics of degree L = 2n − 1 or less, so that, for a given L, a number of n = (L + 1)/2 integration points is needed.
In PAMoC, radial integration by the Gauss-Legendre quadrature rule combined with Becke and Ahlrichs transformations of the radial coordinate, can be selected by the keywords "radrule 15", "radrule 16", and "radrule 17", respectively.

Becke, Ahlrichs, and linear grids, evaluated using the roots (and the associated weights) of the Legendre polynomials, are reported in Tables 3.2 and 3.3 for n = 11, and are compared in Figure 8.1 with the analogous grids obtained using the roots (and the associated weights) of the Chebyshev polynomials of the second kind.

Table 3.2 − Roots of the n-point Gauss-Legendre quadrature rule, q_i, combined with Becke, Ahlrichs, and linear grids, r_i ≡ r(q_i).					Table 3.3 − Weights^(a) of the n-point Gauss-Legendre quadrature rule, w_i, combined with Becke, Ahlrichs, and linear grids, ν_i.
i	Gauss-Legendre	Becke^(a)	Ahlrichs^(a)	Linear^(b)	i	Gauss-Legendre	Becke^(b)	Ahlrichs^(b)	Linear^(c)
1	−0.9782	0.0110	0.0016	0.1089	1	(-2)5.567	(-6)3.450	(-8)2.000	(-3)3.298
2	−0.8871	0.0598	0.0227	0.5647	2	(-1)1.256	(-4)2.526	(-5)2.108	(-1)2.002
3	−0.7302	0.1560	0.0953	1.3492	3	(-1)1.863	(-3)3.028	(-3)1.001	(+0)1.696
4	−0.5191	0.3166	0.2557	2.4045	4	(-1)2.332	(-2)2.025	(-2)1.420	(+0)6.741
5	−0.2695	0.5754	0.5431	3.6523	5	(-1)2.628	(-1)1.080	(-1)1.075	(+1)1.753
6	0.0000	1.0000	1.0000	5.0000	6	(-1)2.729	(-1)5.459	(-1)5.575	(+1)3.412
7	0.2695	1.7380	1.6768	6.3477	7	(-1)2.628	(+0)2.976	(+0)2.270	(+1)5.295
8	0.5191	3.1588	2.6425	7.5955	8	(-1)2.332	(+1)2.012	(+0)7.977	(+1)6.727
9	0.7302	6.4116	4.0153	8.6508	9	(-1)1.863	(+2)2.103	(+1)2.649	(+1)6.971
10	0.8871	16.7089	6.0694	9.4353	10	(-1)1.256	(+3)5.497	(+1)9.543	(+1)5.590
11	0.9782	90.8639	8.8199	9.8911	11	(-2)5.567	(+6)1.939	(+2)5.516	(+1)2.723
(a) R = 1 and r₀ = 0. (b) a = 0 and b = 10.					(a) The weights are given in scientific notation, the power of ten being shown in parentheses. (b) R = 1 and r₀ = 0. (c) a = 0 and b = 10.

4. Gauss-Laguerre quadrature

Gauss-Laguerre quadrature provides an approximate solution to the definite integral of a function e^−q f(q) over the interval [0, +∞] as a weighted sum of function values at specified points within the domain of integration:

+∞ ∫ 0 e^−q f(q) dq ≈ n ∑ i=1 w_i f(q_i)

(4.1)

It fits all polynomials of degree (2n − 1). The evaluation points q_i for quadrature order n are just the roots of the Laguerre polynomials L_n(q), with associated weight w_i.

**Table 4.1** − First six Laguerre polynomials with associated roots and weights.
L_n(q) = n ∑ k=0 ( n k ) (−1)^k / k! q^k	q_i	w_i = q_i / (n + 1)² [ L_n+1(q_i) ]²
L₀(q) = 1
L₁(q) = −q + 1	q₁ = 1	w₁ = 1
L₂(q) = ½(q² − 4q + 2)	q₁ = 2 − √2 = 0.585786	w₁ = ¼(2 + √2) = 0.853553
L₂(q) = ½(q² − 4q + 2)	q₂ = 2 + √2 = 3.41421	w₂ = ¼(2 − √2) = 0.146447
L₃(q) = ⅙(−q³ + 9q² − 18q + 6)	q₁ = 0.415775	w₁ = 0.711093
	q₂ = 2.29428	w₂ = 0.278518
	q₃ = 6.28995	w₃ = 0.010389
L₄(q) = 1 / 24 (q⁴ − 16q³ + 72q² − 96q + 24)	q₁ = 0.322548	w₁ = 0.603154
	q₂ = 1.74576	w₂ = 0.357419
	q₃ = 4.53662	w₃ = 0.038888
	q₄ = 9.39507	w₄ = 0.000539
L₅(q) = 1 / 120 (−q⁵ + 25q⁴ − 200q³ + 600q² − 600q + 120)	q₁ = 0.26356	w₁ = 0.521756
	q₂ = 1.4134	w₂ = 0.398667
	q₃ = 3.59643	w₃ = 0.075942
	q₄ = 7.08581	w₄ = 0.003612
	q₅ = 12.6408	w₅ = 0.000023
L₆(q) = 1 / 720 (q⁶ − 36q⁵ + 450q⁴ − 2400q³ + 5400q² − 4320q + 720)	q₁ = 0.222847	w₁ = 0.458965
	q₂ = 1.188932	w₂ = 0.417001
	q₃ = 2.992736	w₃ = 0.113373
	q₄ = 5.775144	w₄ = 0.010399
	q₅ = 9.837467	w₅ = 0.000261
	q₆ = 15.98287	w₆ = 0.000001

Radial integral. PAMoC can use the Gauss-Laguerre rule to estimate the radial integral (2.11), provided that the keyword "radrule" is set to 47. Expressing the radial coordinate as a linear function of an adjustable scale factor R,

r = r₀ + R q ≡ r(q) ⇒ dr = R dq,

(4.2)

yields:

+∞ ∫ 0 r² g(r) dr = +∞ ∫ 0 R r² e^−q e^+q g[r(q)] dq = +∞ ∫ 0 e^−q G(q) dq ≈
≈ n ∑ i=1 w_i G(q_i) = n ∑ i=1 w_i R r_i² e^q_i g(r_i) = n ∑ i=1 ν_i g(r_i)

(4.3)

where G(q) = R r² e^q g(r), and r_i and v_i define the Laguerre grid:

r_i = r₀ + R q_i ν_i = R r_i² e^q_i w_i = R r_i² q_i e^q_i (n + 1)² [L_n+1(q_i)]²

(4.4)

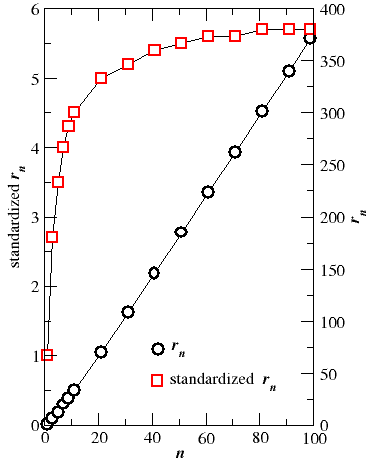
highest root <i>r<sub>n</sub></i> of Laguerre polynomials versus the
number <i>n</i> of their roots — **Figure 4.1:** Dependence of the value of the highest radial coordinate, *r_n*, on the number n of roots of the Laguerre polynomial.

As the number of quadrature points n increases, the value of r_n increases accordingly (i.e. r_n ≈ −12.58 + 3.87 n for n > 20, cf Figure 4.1). As discussed in § 10 about the Handy grid, also the roots of the Laguerre polynomial comprise a number of points which are very far from the nucleus, and which probably contribute very little to the radial integral. Usually a distance of 10 bohr is large enough to be a good approximation to infinity, so that points beyond this value can be neglected. The percentage of roots lower than 10 bohr is about [539 ln(n) − 616]/n (that is less than 50% for n = 21) and decreases approximately as 2633/(37 + n). This waste of evaluation points can be avoided by using a scaling factor in the manner described in § 2.3.4. PAMoC expresses the scaling parameter R as the product of two factors, namely, the covalent radius of the atom, R_cov, times a parameter σ, the value of which is chosen so that the the middle root of the quadrature is equal to R_cov. The resulting values, for R_cov = 1, are the standardized roots and weights defined by Gill and Chien.[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003,24, 732-740.] Figure 4.1 shows that also the value of the highest standardized root r_n increases with n, but it seems to reach an asymptotic value r_asymp of about 5.7 units for n > 80. This fact suggests to scale the radial coordinate furtherly by the factor r_∞/r_asymp, that moves the asymptote closer to r_∞, i.e. a value which is large enough to be a good approximation to infinity. In PAMoC the type of standardization of the radial coordinate is controlled by the keyword "stdtyp", which is 0 for no standardization, 1 for middle-root standardization, and 3 for middle-root standardization with additional correction by the nearest integer of the multiplying factor r_∞/r_asymp.

Gill and Chien pointed out that the Laguerre grid (4.4) is exact if G(q) = L_2n−1(q), which implies that

g(r) = R⁻¹ r⁻² exp(− r − r₀ R ) L_2n−1( r − r₀ R )

(4.5)

"The grid also works well when eq. (4.4) is approximately true, but it becomes less satisfactory when g(r) either decays more slowly than an exponential or contains multiple exponential components with significantly different rates of decay."[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.]

As a test, the radial integrals of the two functions g_gauss(r) = exp(−r²) and g_expon(r) = exp(−r), whose exact values are √π/4 ≈ 0.44311346272637897 and 2, respectively, were esimated by the Laguerre rule. With non-standardized roots and weights, g_expon(r) was integrated exactly by the 2-point formula, whereas g_gauss(r) needed the 49-point grid to reach an accuracy of 7.0 (that is essentially the number of correct digits in the quadrature result). In the latter case the summation converged at the 9th evaluation point, so that the remaining 40 points were calculated unnecessarily. On the contrary, using standardized roots and weights, the Gaussian function is integrated by the 11-point quadrature formula with accuracy 6.8 and almost exactly by the 15-point grid (accuracy 11.1), whereas the radial integral of the exponential function is roughly approximated even by the 99-point quadrature formula (accuracy 1.1). The additional correction of the standardizing parameter by the integer factor 2 (corresponding to the value of the ratio r_∞/r_asymp) does not facilitate the integration of the Gaussian function, since 18 points are needed for an accuracy of 10.0, but yields an accuracy of 6.7 for the 5-point quadrature of the exponential function.

5. Generalized Gauss-Laguerre quadrature

GeneralizedGauss-Laguerre quadrature provides an approximate solution to the definite integral of a function q^α e^−q f(q) over the interval [0, +∞] and for some real number α > −1 as a weighted sum of function values at specified points within the domain of integration:

+∞ ∫ 0 q^α e^−q f(q) dq ≈ n ∑ i=1 w_i f(q_i)

(5.1)

It fits all polynomials of degree (2n − 1). The evaluation points q_i for quadrature order n are just the roots of the generalized Laguerre polynomial L_n^(α)(q), with associated weight w_i.

**Table 5.1** − First three generalized Laguerre polynomials with associated roots
L_n^(α)(q) = n ∑ k=0 ( n + α n − k ) (−1)^k / k! q^k	q_i
L₀^(α)(q) = 1
L₁^(α)(q) = −q + α + 1	q₁ = α + 1
L₂^(α)(q) = ½[q² − (α + 2)(2q − α − 1)]	q₁ = (α + 2) − √α + 2
L₂^(α)(q) = ½[q² − (α + 2)(2q − α − 1)]	q₂ = (α + 2) + √α + 2
L₃^(α)(q) = ⅙{−q³ + (α + 3) [3q² − 3(α + 2)q + (α + 1)(α + 2)]}	…

Radial integral. PAMoC can use the Generalized Gauss-Laguerre rule to estimate the radial integral (2.11), provided that the keyword "radrule" is set to 57. Expressing the radial coordinate as a function of an adjustable scale factor R, as in eq. (4.2), yields:

+∞ ∫ 0 r² g(r) dr = +∞ ∫ 0 R r² q^−α q^α e^−q e^+q g(r) dq = +∞ ∫ 0 q^α e^−q G(q) dq ≈
≈ n ∑ i=1 w_i G(q_i) = n ∑ i=1 w_i R r_i² q_i^−α e^q_i g(r_i) = n ∑ i=1 ν_i g(r_i)

(5.2)

where G(q) = R r² q^−α e^q g(r_i), and r_i and ν_i define the generalized Laguerre grid:

r_i = r₀ + R q_i ν_i = R r_i² q_i^−α e^q_i w_i

(5.3)

It is worth noting that, for r₀ = 0 and α = 2, the expression of the quadrature weights simplifies to ν_i = R³ e^q_i w_i. In this case, the generalized Laguerre grid (5.3) is exact if g(r) = R⁻³ exp(−r/R) L_2n−1⁽²⁾(r/R).

q_i and r_i (σ = 1)	σ = ¹⁄_q₆	σ = ²⁄_q₆	q_i and r_i (σ = 1)	σ = ¹⁄_q₆	σ = ²⁄_q₆	w_i	σ = 1	σ = ¹⁄_q₆	σ = ²⁄_q₆	w_i	σ = 1	σ = ¹⁄_q₆	σ = ²⁄_q₆
Table 5.2 − Roots^(a) of the 11-point Gauss-Laguerre and Generalized Gauss-Laguerre (α = 2) quadrature rules, q_i and standardized r_i ≡ r(q_i).						Table 5.3 − Weights^(a,b) of the 11-point Gauss-Laguerre and Generalized Gauss-Laguerre (α = 2) quadrature rules, w_i and standardized ν_i.
Gauss-Laguerre			Generalized Gauss-Laguerre			Gauss-Laguerre				Generalized Gauss-Laguerre
0.1258	0.0168	0.0335	0.5298	0.0555	0.1666	(-1)2.85	(-3)5.11	(-5)1.21	(-5)9.66	(-1)2.85	(-3)5.11	(-5)1.21	(-5)9.66
0.6654	0.0886	0.1772	1.4318	0.1501	0.4502	(-1)3.90	(-1)3.36	(-4)7.93	(-3)6.34	(-1)3.90	(-1)3.36	(-4)7.93	(-3)6.34
1.6472	0.2193	0.4387	2.7533	0.2886	0.8657	(-1)2.33	(+0)3.28	(-3)7.74	(-2)6.19	(-1)2.33	(+0)3.28	(-3)7.74	(-2)6.19
3.0911	0.4116	0.8232	4.5189	0.4736	1.4208	(-2)7.66	(+1)1.61	(-2)3.80	(-1)3.04	(-2)7.66	(+1)1.60	(-2)3.80	(-1)3.04
5.0293	0.6697	1.3394	6.7643	0.7010	2.1268	(-2)1.44	(+1)5.56	(-1)1.31	(+0)1.05	(-2)1.44	(+1)5.56	(-1)1.31	(+0)1.05
7.5099	1.0000	2.0000	9.5412	1.0000	3.0000	(-3)1.52	(+2)1.56	(-1)3.69	(+0)2.95	(-3)1.52	(+2)1.56	(-1)3.69	(+0)2.95
10.6060	1.4123	2.8245	12.9259	1.3548	4.0649	(-5)8.51	(+2)3.87	(-1)9.13	(+0)7.30	(-5)8.51	(+2)3.87	(-1)9.13	(+0)7.30
14.4316	1.9217	3.8434	17.0367	1.7856	5.3568	(-6)2.29	(+2)8.84	(+0)2.09	(+1)1.67	(-6)2.29	(+2)8.84	(+0)2.09	(+1)1.67
19.1789	2.5538	5.1076	22.0710	2.3132	6.9397	(-8)2.00	(+3)1.95	(+0)4.61	(+1)3.69	(-8)2.00	(+3)1.95	(+0)4.61	(+1)3.69
25.2177	3.3579	6.7159	28.4079	2.9774	8.9322	0	(+3)4.39	(+1)1.04	(+1)8.29	0	(+3)4.39	(+1)1.04	(+1)8.29
33.4972	4.4604	8.9208	37.0190	3.8799	11.6398	0	(+4)1.14	(+1)2.70	(+2)2.16	0	(+4)1.14	(+1)2.70	(+2)2.16
(a) R = 1 and r₀ = 0.						(a) R = 1 and r₀ = 0. (b) The weights are given in scientific notation, the power of ten being shown in parentheses.

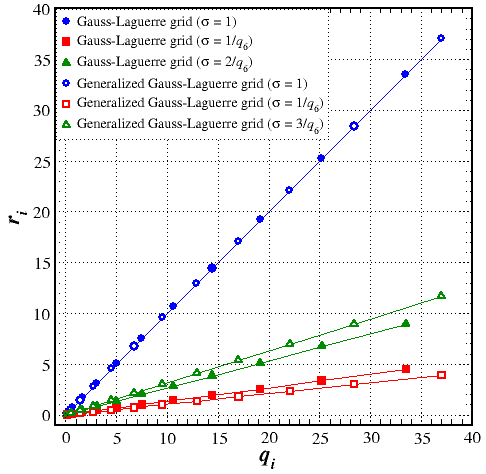
Comparison of Laguerre and Generalized Laguerre grids — **Figure 5.1:** Comparison of Gauss-Laguerre (full symbols) and Generalized Gauss-Laguerre (α = 2; open symbols) 11-point grids with no standardization (blue circles, σ = 1), with Gill-Chien standardization (red squares, σ = 1/q₆),[10Gill, P. M. W.; Chien, S.-H.
*J. Comput. Chem.* **2003**, 24, 732-740.] and with corrected standardization (dark green triangles, σ = 2/q₆ and σ = 3/q₆).

6. Gauss-Hermite quadrature

Gauss-Hermite quadrature provides an approximate solution to the integral of a function e^-q² f(q) over the interval [−∞, +∞] as a weighted sum of function values at specified points

+∞ ∫ −∞ e^-q² f(q) dq ≈ n ∑ i=1 w_i f(q_i)

(6.1)

where n is the number of sample points used. The q_i are the roots of the Hermite polynomial H_n(q) with associated weights w_i.

**Table 6.1** − First four Hermite polynomials with associated roots and weights.
H_n(q) = (−1)ⁿ e^q² dⁿ / dqⁿ e^−q² = = n! ⌊n/2⌋ ∑ k=0 (−1)^k (2 q)^n−2k / k! (n − 2k)!	q_i	w_i = 2ⁿ⁻¹ n! √π / n² [ H_n−1(q_i) ]²
H₀(q) = 1
H₁(q) = 2q	q₁ = 0	w₁ = √π = 1.772454
H₂(q) = 4q² − 2	q_1,2 = ∓√½ = ∓0.707107	w_1,2 = ½√π = 0.886002
H₃(q) = 8q³ − 12q	q_1,3 = ∓√(³⁄₂) = ∓1.224745	w_1,3 = 0.295409
H₃(q) = 8q³ − 12q	q₂ = 0	w₂ = 1.181636
H₄(q) = 16q⁴ − 48q² + 12	q_1,3 = ∓√[(3+√6)/2] = ∓1.650680	w_1,3 = 0.081313
H₄(q) = 16q⁴ − 48q² + 12	q_2,4 = ∓√[(3-√6)/2] = ∓0.524648	w_2,4 = 0.804914

Multipole moments of the overlap density between two GTO's. Stone pointed out that the unabridged Cartesian multipole moments of the overlap density between two cartesian Gaussian type orbitals (GTO's) can be efficiently and accurately estimated using Gauss-Hermite quadrature.[22Stone, A. J.
J. Chem. Theory Comput. 2005, 1, 1128-1132.] The following integrals are needed:

S_{μ∊A,ν∊B}^(l,m,n)(A) = <χ_μ^A|x_A^l y_A^m z_Aⁿ|χ_ν^B> = +∞ ∫ −∞ x_A^l y_A^m z_Aⁿ χ^*_μ^A(r) χ_ν^B(r) d³r,

(6.2))

where

χ_μ^A(r) = N₁ x_A^l₁ y_A^m₁ z_A^n₁ exp(-ζ₁ r_A²) χ_ν^B(r) = N₂ x_B^l₂ y_B^m₂ z_B^n₂ exp(-ζ₂ r_B²)

(6.3)

r_A = r − A and r_B = r − B are the electron positions relative to the positions of atoms A and B on which the GTO's are centered, ζ₁ and ζ₂ are the exponents, and N₁ and N₂ are normalization constants.

Boys[23Boys, S. F.
Proc. Roy. Soc. A 1950, 200, 542-554.] showed that the product of two 1s GTO's, one centered at A and the other centered at B, is another Gaussian centered at P = ζ₁A + ζ₂B / ζ₁ + ζ₂ with exponent ζ₃ = ζ₁ + ζ₂:

exp(−ζ₁ r_A²) ⋅ exp(−ζ₂ r_B²) = exp[− ζ₁ ζ₂ ζ₃ (A − B)²] ⋅ exp(− ζ₃ r_P²) ≡ K_AB exp(− ζ₃ r_P²),

(6.4)

where K_AB = exp[− ζ₁ ζ₂ / ζ₃ (A − B)²] and r_P = r − P. Since 1s GTO's are separable along the three Cartesian coordinates:

exp(− ζ₃ r_P²) = exp(− ζ₃ x_P²) ⋅ exp(− ζ₃ y_P²) ⋅ exp(− ζ₃ z_P²),

(6.5)

the integral S_{μ∊A,ν∊B}^(l,m,n)(A) can be written as:

S_{μ∊A,ν∊B}^(l,m,n)(A) = N₁ N₂ K_AB ∏ (t; k, k₁, k₂) +∞ ∫ −∞ G_A(t; k, k₁, k₂) dt,

(6.6)

where

G_A(t; k, k₁, k₂) = (t − A_t)^k+k₁ (t − B_t)^k₂ exp[−ζ₃(t − P_t)² = t_A^k+k₁ t_B^k₂ exp[−ζ₃t_P²],

(6.7)

for (t; k, k₁, k₂) = (x; l, l₁, l₂), (y; m, m₁, m₂), and (z; n, n₁, n₂). As the integrand G_A(t) doesn't exactly correspond to the integrand of the quadrature formula, we need a change of variable

q = √ζ₃ (t − P_t) ⇔ t = ^q⁄_√ζ₃ + P_t ⇒ dt = (¹⁄_√ζ₃) dq,

(6.8)

which, coupled with the integration by substitution, yields for each integral in eq. (6.6):

+∞ ∫ −∞ G_A(t) dt = +∞ ∫ −∞ (¹⁄_√ζ₃) (^q⁄_√ζ₃ + P_t - A_t)^k+k₁ (^q⁄_√ζ₃ + P_t - B_t)^k₂ exp(−q²) dq =
= +∞ ∫ −∞ F_A(q) exp(−q²) dq ≈ n ∑ i=1 w_i F_A(q_i) =
= n ∑ i=1 (^w_i⁄_√ζ₃) (^q_i⁄_√ζ₃ + P_t - A_t)^k+k₁ (^q_i⁄_√ζ₃ + P_t - B_t)^k₂ = n ∑ i=1 (^w_i⁄_√ζ₃) (t_i − A_t)^k+k₁ (t_i − B_t)^k₂

(6.9)

where q_i are the roots of the Hermite polynomial of order n and w_i are the associated weights. The coordinates t_i are defined in terms of the roots q_i, according to transformation (6.8).

The n-point Gauss-Hermite rule integrates exactly all polynomials of degree (2 n − 1) or less. Since the integrand F_A(q) in eq. (6.9) is a polynomial of degree (k + k₁ + k₂), a number n = (k + k₁ + k₂)/2 is needed.

It is worth noting that in the case of monocentric integrals we have

S_{μ∊A,ν∊A}^(l,m,n)(A) = <χ_μ^A|x_A^l y_A^m z_Aⁿ|χ_ν^A> = N₁ N₂ ∏ t=x,y,z +∞ ∫ −∞ t_A^k+k₁+k₂ exp[-ζ₃t_A²] dt,

(6.10)

where (k+k₁+k₂) = (l+l₁+l₂), (m+m₁+m₂), (n+n₁+n₂) for t = x, y, z, respectively. For even (k+k₁+k₂) an analytical solution is available for the integral

+∞ ∫ −∞ t_A^k+k₁+k₂ exp[-ζ₃t_A²] dt = ( π ζ₃ )^½ (k+k₁+k₂−1)!! (2 ζ₃)^{(k+k₁+k₂)/2} ^,

(6.11)

whereas for odd (k+k₁+k₂) the integral is equal to zero. The final expression for the Mulliken unabridged cartesian multipole moments of atom A is

m_A^(l,m,n) = ∑ μ∊A ∑ B ∑ ν∊B D_μν^AB S_{μ∊A,ν∊B}^(l,m,n)(A).

(6.12)

The procedure outlined above is implemented in PAMoC routines muldma.f and stodma.f.

Radial integral. PAMoC can use the Gauss-Hermite rule to estimate the radial integral (2.11), provided that the keyword "radrule" is set to 67. Expressing the radial coordinate as a function of an adjustable scale factor R, as in eq. (4.2), yields:

¹⁄₂ +∞ ∫ −∞ r² g(r) dr = +∞ ∫ −∞ ¹⁄₂ R r² e^−q² e^+q² g(r) dq = +∞ ∫ −∞ e^−q² G(q) dq ≈
≈ n ∑ i=1 w_i G(q_i) = n ∑ i=1 ¹⁄₂ w_i R r_i² e^q_i² g(r_i) = n ∑ i=1 ν_i g(r_i)

(6.13)

where G(q) = ¹⁄₂ R r² e^q² g(r), and r_i and ν_i define the Hermite grid:

r_i = r₀ + R q_i ν_i = ¹⁄₂ R r_i² e^q_i² w_i

(6.14)

It is worth noting that, for r₀ = 0, the expression of the quadrature weights simplifies to ν_i = ¹⁄₂ R³ e^q_i² w_i. In this case, the Hermite grid (6.14) is exact if g(r) = 2 R⁻³ exp(−r²/R) H_2n−1(r/R).

8. Gauss-Chebyshev quadrature of the second kind

Gauss-Chebyshev quadrature of the second kind provides an approximate solution to the definite integral of a function √1 − q² f(q) over the interval [−1, +1] as a weighted sum of function values at specified points within the domain of integration:

+1 ∫ −1 √1 − q² f(q) dq ≈ n ∑ i=1 w_i f(q_i)

(8.1)

It fits all polynomials of degree (2n − 1). The evaluation points q_i for quadrature order n are just the roots of the Chebyshev polynomial of the second kind U_n(q), with associated weight w_i.

**Table 8.1** − First nine Chebyshev polynomials of the second kind with associated roots and weights.
U_n(q) = ⌊n/2⌋ ∑ k=0(-1)^k ( n − k k ) (2q)^n−2k	q_i = cos ( i / n + 1π )	w_i = π / n + 1 sin² ( i / n + 1π ) = π / n + 1 (1 − q_i²)
U₀(q) = 1
U₁(q) = 2 q	q₁ = 0	w₁ = π/2
U₂(q) = 4 q² − 1	q_1,2 = ±¹⁄₂	w_1,2 = π/4
U₃(q) = 8 q³ − 4 q	q₂ = 0 q_1,3 = ±1/√2	w₂ = π/4 w_1,3 = π/8
U₄(q) = 16 q⁴ − 12 q² + 1	q_1,2,3,4 = ±√(3 ± √5)/8	w_1,2 = π(5 − √5)/40 w_3,4 = π(5 + √5)/40
U₅(q) = 32 q⁵ − 32 q³ + 6 q	q₃ = 0 q_1,5 = ±0.866025 q_2,4 = ±0.5	w₃ = 0.523599 w_1,5 = 0.130900 w_2,4 = 0.392699
U₆(q) = 64 q⁶ − 80 q⁴ + 24 q² − 1	q_1,6 = ±0.900969 q_2,5 = ±0.623490 q_3,4 = ±0.222521	w_1,6 = 0.084489 w_2,5 = 0.274333 w_3,4 = 0.426576
U₇(q) = 128 q⁷ − 192 q⁵ + 80 q³ − 8 q	q₄ = 0 q_1,7 = ±0.923880 q_2,6 = ±0.707107 q_3,5 = ±0.382683	w₄ = 0.392699 w_1,7 = 0.057509 w_2,6 = 0.196350 w_3,5 = 0.335190
U₈(q) = 256 q⁸ − 448 q⁶ + 240 q⁴ − 40 q² + 1	q_1,8 = ±0.939693 q_2,7 = ±0.766044 q_3,6 = ±0.5 q_4,5 = ±0.173648	w_1,8 = 0.040833 w_2,7 = 0.144226 w_3,6 = 0.261799 w_4,5 = 0.338540
U₉(q) = 512 q⁹ − 1024 q⁷ + 672 q⁵ − 160 q³ + 10 q	q₅ = 0 q_1,9 = ±0.951057 q_2,8 = ±0.809017 q_3,7 = ±0.587785 q_4,6 = ±0.309017	w₅ = 0.314159 w_1,9 = 0.029999 w_2,8 = 0.108539 w_3,7 = 0.205620 w_4,6 = 0.284160
The floor function ⌊n/2⌋ specifies the largest integer less than or equal to n/2.

The Chebyshev polynomials of the second kind are orthogonal with respect to the weight function √1 − q² over the interval [−1, +1], i.e.:

+1 ∫ −1 U_n(q) U_m(q) √1 − q² dq = π 2 δ_nm

(8.2)

As a consequence:

n ∑ i=1 w_i = π 2

(8.3)

Radial integral. The Gauss-Chebyshev second kind quadrature can be used to estimate the radial integral (2.11), provided that a suitable variable transformation is given to map the improper interval [0, ∞] to a finite interval [−1, +1].

Becke's grid. In 1988, Becke introduced the transformation:[2Becke, A. D.
J. Chem. Phys. 1988, 88, 2547-2553.]

r = r₀ + R 1 + q 1 − q ≡ r(q) ⇒ dr = 2 R (1 − q)² dq = 2 r − r₀ 1 − q² dq

(8.4)

The displacement of the origin from 0 to r₀ was not considered in the original paper, but has been added here for completeness. At q = − 1, r(q) = r₀, and as q → 1, the sample points tend toward infinity. Under this map, the radial integral becomes:

+∞ ∫ 0 r² g(r) dr = +1 ∫ −1 2 r² (r − r₀) 1 − q² g(r) dq = +1 ∫ −1 √1 − q² G(q) dq ≈
≈ n ∑ i=1 w_i G(q_i) = n ∑ i=1 2 w_i r_i² (r_i − r₀) (1 − q_i²)^3/2 g(r) = n ∑ i=1 ν_i g(r_i)

(8.5)

where G(q) = 2 r² (r − r₀) / (1 − q²)^3/2 g(r), and r_i and ν_i define the Becke grid:

r_i = r₀ + R 1 + q_i 1 − q_i ν_i = 2 r_i² (r_i − r₀) (1 − q_i²)^3/2 w_i = 2π n + 1 r_i² (r_i − r₀) √1 − q_i² q_i = cos ( i n + 1 π) ∀ i = 1, 2, ..., n

(8.6)

At q = 0, r(0) − r₀ = R and, in particular, q_(n+1)/2 = 0 ∀ n odd, i.e. the middle root of the Becke grid is equal to R. Thus, for R = 1, eq. (8.6) gives standardized roots and weights, as defined by Gill and Chien.[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.]. The value of the scale factor R controls the extent of the integrand. Becke chose R as half of the Bragg-Slater radius of the respective atom, except for hydrogen in which case the factor 1/2 is not applied.[2Becke, A. D.
J. Chem. Phys. 1988, 88, 2547-2553.] The Becke grid (8.6) is exact if G(q) = U_2n−1(q), which implies

g(q) = R³ 4 r^3/2 (r + R)³ U_2n−1( r − R r + R )

(8.7)

In general, such g(r) possess a 1/r^3/2 singularity at the origin and decay as 1/r^9/2 at large r.

Ahlrichs's grid. In 1995, Treutler and Ahlrichs introduced the transformation:[7Treutler, O.; Ahlrichs, R.
J. Chem. Phys. 1995, 102, 346-354.]

r = r₀ − R ln 2 (1 + q)^α ln 1 − q 2 ≡ r(q) ⇒ dr = (r − r₀) ( α 1 + q − 1 1 − q ln⁻¹ 1 − q 2 ) dq

(8.8)

which is normalized to map the center of the q interval onto r(0) - r = R. At q = −1, r(q) − r₀ = 0, and as q → 1, the sample points tend toward infinity. Under this map, the radial integral becomes:

+∞ ∫ 0 r² g(r) dr = +1 ∫ −1 r² (r − r₀) ( α 1 + q − 1 1 − q ln⁻¹ 1 − q 2 ) √1 − q² √1 − q² g(r) dq = +1 ∫ −1 √1 − q² G(q) dq
≈ n ∑ i=1 w_i G(q_i) = n ∑ i=1 π n + 1 (1 − q_i²) G(q_i)
= n ∑ i=1 π n + 1 r_i² (r_i − r₀) ( α√ 1 − q_i 1 + q_i − √ 1 + q_i 1 − q_i ln⁻¹ 1 − q_i 2 ) g(r) = n ∑ i=1 ν_i g(r_i)

(8.9)

where r_i and ν_i, with α = 0.6, define the Ahlrichs grid:

r_i = r₀ − R ln 2 (1 + q_i)^α ln 1 − q_i 2 ν_i = r_i² (r_i − r₀) ( α 1 + q_i − 1 1 − q_i ln⁻¹ 1 − q_i 2 ) w_i √1 − q_i²
= π n + 1 r_i² (r_i − r₀) [ α √ 1 − q_i 1 + q_i − √ 1 + q_i 1 − q_i ln⁻¹ 1 − q_i 2 ] q_i = cos ( i n + 1 π) ∀ i = 1, 2, ..., n

(8.10)

Linear grid. Although it is rather inappropriate for radial integration, the linear transformation (3.2) can also be used in combination with the 2nd kind Gauss-Chebyshev quadrature rule, yielding the following quadrature points and weights:

r_i = b − a / 2 q_i + a + b / 2
ν_i = b − a / 2 √1 − q² r_i² w_i = π (b − a) / 2 (n + 1) r_i² √1 − q² ∀ i = 1, 2, ..., n	(8.11)
with q_i = cos ( i / n + 1π)

Becke, Ahlrichs, and linear grids, evaluated using the roots (and the associated weights) of the Chebyshev polynomials of the second kind, are reported in Tables 8.2 and 8.3 for n = 11, and are compared in Figure 8.1 with the analogous grids obtained using the roots (and the associated weights) of the Legendre polynomials.

Table 8.2 − Roots of the n-point Gauss-Chebyshev quadrature rule of the second kind, q_i, combined with Becke, Ahlrichs, and linear grids, r_i ≡ r(q_i).					Table 8.3 − Weights^(a) of the n-point Gauss-Chebyshev quadrature rule of the second kind, w_i, combined with Becke, Ahlrichs, and linear grids, ν_i.
i	2nd kind Gauss-Chebyshev	Becke^(a)	Ahlrichs^(a)	Linear^(b)	i	2nd kind Gauss-Chebyshev	Becke^(b)	Ahlrichs^(b)	Linear^(c)
1	−0.9659	0.0173	0.0033	0.1704	1	(-2)1.754	(-5)1.053	(-7)1.100	(-3)9.834
2	−0.8660	0.0718	0.0299	0.6699	2	(-2)6.545	(-4)3.876	(-5)4.292	(-1)2.937
3	−0.7071	0.1716	0.1093	1.4645	3	(-1)1.309	(-3)3.740	(-3)1.391	(+0)1.985
4	−0.5000	0.3333	0.2738	2.5000	4	(-1)1.963	(-2)2.239	(-2)1.637	(+0)7.085
5	−0.2588	0.5888	0.5581	3.7059	5	(-1)2.443	(-1)1.106	(-1)1.110	(+1)1.736
6	0.0000	1.0000	1.0000	5.0000	6	(-1)2.618	(-1)5.236	(-1)5.348	(+1)3.272
7	0.2588	1.6984	1.6442	6.2941	7	(-1)2.443	(+0)2.656	(+0)2.063	(+1)5.009
8	0.5000	3.0000	2.5508	7.5000	8	(-1)1.963	(+1)1.632	(+0)6.934	(+1)6.377
9	0.7071	5.8284	3.8201	8.5355	9	(-1)1.309	(+2)1.466	(+1)2.197	(+1)6.743
10	0.8660	13.9282	5.6704	9.3301	10	(-2)6.545	(+3)2.830	(+1)7.357	(+1)5.697
11	0.9659	57.6955	8.8138	9.8296	11	(-2)1.754	(+5)3.885	(+2)3.485	(+1)3.273
(a) R = 1 and r₀ = 0. (b) a = 0 and b = 10.					(a) The weights are given in scientific notation, the power of ten being shown in parentheses. (b) R = 1 and r₀ = 0. (c) a = 0 and b = 10.

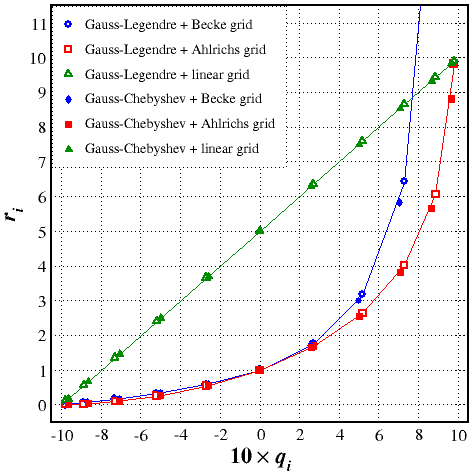
In PAMoC, radial integration by the 2nd kind Gauss-Chebyshev quadrature rule combined with Becke, Ahlrichs, and linear transformations of the radial coordinate, can be selected by the keywords "radrule 25", "radrule 26", and "radrule 27", respectively.

9. Gauss-Gill quadrature

The Gauss-Gill quadrature provides an approximate solution to the definite integral of a function ln² q f(q) over the interval [0, 1] as a weighted sum of function values at specified points within the domain of integration:[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.]

1 ∫ 0 ln² q f(q) dq ≈ n ∑ i=1 w_i f(q_i)

(9.1)

It fits all polynomials of degree (2n − 1). The evaluation points q_i for quadrature order n are the roots of the polynomial Q_n(q) orthogonal on the interval [0, 1] with respect to the weight function ln² q, and w_i are the associated weights.

**Table 9.1** − First three Gill polynomials with associated roots and weights
n	Q_n(q)	q_i	w_i
1	8q − 1	q₁ = 1/8	w₁ = 2.000000000000000
2	7992q² − 4104q + 217	q₁ = 0.059850992523974 q₂ = 0.453662520989539	w₁ = 1.669136108179106 w₂ = 0.330863891820894
3	…	q₁ = 0.036263311146964 q₂ = 0.273148602374171 q₃ = 0.653711089636059	w₁ = 1.363830383647107 w₂ = 0.565815459643824 w₃ = 0.070354156709070

Roots and weights for n = 1-26, 30, 35, 40, 45, 50 can be obtained from Gill's website at the Australian National University (ANU). Their values for n = 1-3 are reported in Table 9.1

MultiExp grid for radial quadrature. The Gauss-Gill "log-squared" quadrature rule (9.1) was devised to estimate the radial integral (2.11), provided that a suitable variable transformation is given to map the improper interval [0, ∞] to a finite interval [0,1]. Gill and Chien proposed the transformation:[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.]

r = r₀ − R ln q ⇒ dr = − R q dq

(9.2)

At q = 1, r(q) = r₀, and as q → 0, the sample points tend toward infinity. Under this map, the radial integral becomes:

+∞ ∫ 0 r² g(r) dr = R 1 ∫ 0 r² q⁻¹ ln⁻²q ln²q g(r) dq = 1 ∫ 0 ln²q G(q) dq ≈
≈ n ∑ i=1 w_i G(q_i) = R n ∑ i=1 r² q_i⁻¹ ln⁻²q_i w_i g(r_i) = n ∑ i=1 ν_i g(r_i)

(9.3)

where

G(q) = R (r₀ − R ln q)² q⁻¹ ln⁻²q g(r) = R³ r² (r − r₀)⁻² e^(r−r₀)/R g(r)

and r_i and ν_i define the MultiExp grid:

r_i = r₀ − R ln q_i ν_i = R (r₀ − R ln q_i)² q_i⁻¹ ln⁻² q_i w_i = R³ r² (r − r₀)⁻² e^(r−r₀)/R w_i

(9.4)

The standardized roots and weights introduced by Gill and Chien[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.] are obtained by using R = R_cov σ_Gill-Chien, with R_cov = 1 and σ_Gill-Chien, = − 1/ln q_(n+1)/2. For example, the standardizing factor for the 3-point quadrature formula is σ_Gill-Chien = − 1/ln q₂ = 0.770570791. The values of σ_Gill-Chien depend on the value of the middle root of the quadrature, q_(n+1)/2, as well as on the number n of evaluation points. In order to avoid such a dependence, the value of q at the center of the interval where q itself is defined, i.e. q_center = ¹⁄₂, can be used to compute the standardizing factor as σ_center = − ln⁻¹(q_center) = ln⁻¹(2) = 1.442695.

The MultiExp grid (9.4) is exact if G(q) = Q_2n−1(q), which implies

g(r) = R⁻³ r⁻² (r − r₀)² e^{−(r−r₀)/R} Q_2n−1(e^{−(r−r₀)/R})

(9.5)

For r₀ = 0, eq. (9.5) can be written as

g(r) = R⁻³ 2n−1 ∑ k=0 c_k e^−(k+1)r/R

(9.6)

Obviously, such g(r) are linear combinations of exponential functions, and for this reason Gill and Chien named "MultiExp" the grid defined by eq. (9.4). These authors concluded that "The accuracy with which a quadrature scheme estimates the value of an integral depends on how close the integrand is to the set of functions for which the quadrature is exact. Our principal interest lies in the development of efficient quadrature schemes for the types of integral that arise in atomic and molecular calculations using density functional theory. Because of shell structure, the radial electron density around an atom can usually be modeled well by a sum of exponential functions with a variety of decay constants. It has previously been noted[3Murray, C. W.; Handy, N. C.; Laming, G. J.
Mol. Phys. 1993, 78, 997-1014.; 7Treutler, O.; Ahlrichs, R.
J. Chem. Phys. 1995, 102, 346-354.] that such multiexponential character may limit the usefulness of the Laguerre grid, but it is clear that the MultiExp grid is well suited to such problems."[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.]

Gauss-Gill quadrature with Knowles, Handy, and linear grids. The Gauss-Gill quadrature can also be used in conjunction with any variable transformation which maps the semi-infinite interval spanned by the radial coordinate r into the finite interval [0, 1] of the variable q. PAMoC can use the transformations due to Knowles[8Mura, M. E.; Knowles, P. J.
J. Chem. Phys. 1996, 104, 9848-9858.] and Handy,[3Murray, C. W.; Handy, N. C.; Laming, G. J.
Mol. Phys. 1993, 78, 997-1014.] which are described in section 10 (eqs. 10.14 and 10.10, respectively) with more details, and of course some linear transformation like eq. (10.23). The appropriate weights for the Gauss-Gill quadrature are given by equations from (9.7) through (9.10), respectively,

Knowles: ν_i = k R r_i² q_i^k−1 / (1 − q_i^k) ln² q_i w_i	(9.7)
Handy: ν_i = m (r_i − r₀) r_i² / q_i (1 − q_i) ln² q_i w_i	(9.8)
modified Handy: ν_i = m (r_max − r₀) r_i² [1 + (r_max − r₀ − 2^m)(1 − q_i)^m−1] q_i^m−1 / [1 + (r_max − r₀ − 2^m) (1 − q_i)^m]² ln² q_i w_i	(9.9)
Linear: ν_i = (r_max − r₀) r_i² / ln² q_i w_i	(9.10)

where q_i and w_i are roots and weights of the Gauss-Gill quadrature rule, and r_i is defined by eqs. (10.14), (10.10), (10.20), and (10.23), respectively.

In PAMoC, radial integration by the MultiExp quadrature is available through the keyword "radrule 31", which actually is the default choice.
Radial integration using Knowles, Handy, and linear grids with the roots and weights of the Gauss-Gill quadrature rule, is afforded through the keywords "radrule 32", "radrule 33", "radrule 34", and "radrule 37", respectively.

Roots and weights of Gauss-Gill quadrature rule combined with the 11-point MultiExp, Knowles' Log3 Handy and linear transformations of the radial coordinate are compared in Tables 9.2 and 9.3, respectively.

**Table 9.2.** − Evaluation Points (*r_i*) of Gauss-Gill quadrature rule combined with different Transformations of the Radial Coordinate.^(a)
	MultiExp^(b)			Knowles' Log3^(b)			Handy^(c)
i	σ = 1	σ = 1.1374	σ = 1.4427	σ = 1	σ = 13.4747	σ = 7.4889	σ = 1	σ = 1.9854	modified Handy^(d)	Linear^(d)
1	0.0455	0.0517	0.0656	0.0000	0.0000	0.0000	0.0000	0.0001	0.0000	0.0530
2	0.1237	0.1407	0.1785	0.0000	0.0007	0.0004	0.0015	0.0029	0.0021	0.3672
3	0.2402	0.2732	0.3465	0.0009	0.0124	0.0069	0.0116	0.0231	0.0161	0.9732
4	0.3995	0.4544	0.5763	0.0063	0.0846	0.0470	0.0511	0.1014	0.0680	1.8430
5	0.6088	0.6924	0.8783	0.0254	0.3416	0.1898	0.1710	0.3394	0.2137	2.9252
6	0.8792	1.0000	1.2685	0.0742	1.0000	0.5558	0.5037	1.0000	0.5645	4.1510
7	1.2292	1.3981	1.7734	0.1756	2.3655	1.3147	1.4234	2.8260	1.3168	5.4401
8	1.6912	1.9235	2.4399	0.3590	4.8379	2.6888	4.1468	8.2331	2.7247	6.7066
9	2.3297	2.6497	3.3611	0.6665	8.9806	4.9912	13.5684	26.9387	4.8570	7.8649
10	3.3044	3.7582	4.7672	1.1710	15.7793	8.7697	57.6650	114.4882	7.2214	8.8364
11	5.2406	5.9604	7.5606	2.0593	27.7479	15.4216	461.8325	916.9235	9.0235	9.5554
(a) R = 1, r₀ = 0, and r_max = 10. (b) The first column (σ = 1) refers to the non-standardized grid, the second column refers to the grid standardized by means of the middle root q_(n+1)/2, and the third column refers to the grid standardized by means of the central point of the interval q_center = ¹⁄₂. (c) The first column refers to the grid standardized by means of the central point of the interval q_center = ¹⁄₂, which yields σ = 1 by definition. The second column refers to the grid standardized by means of the middle root q_(n+1)/2. (d) Non-standardized grid.

The 11-point grids of Table 9.2 are illustrated in Figure 9.1. The effect of standardization is to increase the resolution. This effect is relatively moderate in the case of the MultiExp grid, which has the narrowest range of the grids reported in Table 9.2. The Handy grid is the most extended, with three evaluation points (27%) which are too far to contribute significantly to the integral.

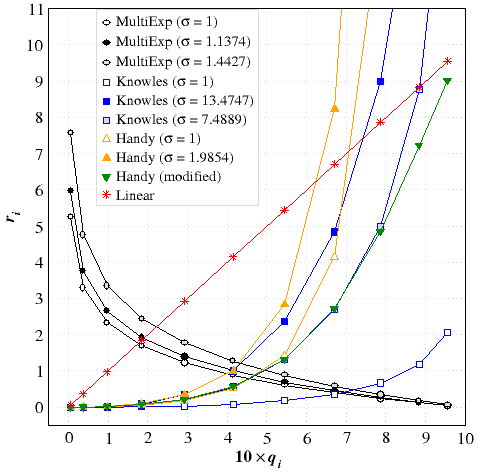
**Figure 9.1:** MultiExp, Knowles' Log3, Handy, and linear transformations of the radial coordinate r = r(q) using the roots, *q_i*, of the 11-point Gauss-Gill quadrature rule (n = 11, r₀ = 0, and *r_max* = 10).

**Table 9.3.** − Weights^(a) (*ν_i*) of Gauss-Gill quadrature rule combined with different Transformations of the Radial Coordinate.
	MultiExp^(b)			Knowles' Log3^(b)			Handy^(c)
i	σ = 1	σ = 1.1374	σ = 1.4427	σ = 1	σ = 13.4747	σ = 7.4889	σ = 1	σ = 1.9854	modified Handy^(d)	Linear^(d)
1	(-4)1.25	(-4)1.83	(-1)3.74	0	0	0	0	0	0	(-4)4.69
2	(-3)1.48	(-3)2.18	(-1)4.45	0	0	0	(-8)1	(-8)6	(-8)2	(-2)6.24
3	(-3)7.90	(-2)1.16	(-1)2.37	0	(-6)4.41	(-7)7.6	(-6)2.66	(-5)2.08	(-6)6.94	(-1)7.05
4	(-2)2.92	(-2)4.29	(-1)8.76	(-7)4.0	(-4)9.76	(-4)1.68	(-4)1.75	(-3)1.37	(-4)3.98	(+0)3.35
5	(-1)8.80	(-1)1.30	(-1)2.64	(-5)1.97	(-2)4.83	(-3)8.29	(-3)5.63	(-2)4.41	(-2)1.02	(+0)9.98
6	(-1)2.37	(-1)3.48	(-1)7.11	(-4)3.90	(-1)9.54	(-1)1.64	(-1)1.34	(+0)1.05	(-1)1.63	(+1)2.19
7	(-1)6.04	(-1)8.87	(+0)1.81	(-3)4.21	(+1)1.03	(+0)1.77	(+0)3.00	(+1)2.35	(+0)1.80	(+1)3.82
8	(+0)1.53	(+0)2.25	(+0)4.60	(-2)3.05	(+1)7.47	(+1)1.28	(+1)7.92	(+2)6.20	(+1)1.33	(+1)5.52
9	(+0)4.15	(+0)6.11	(+1)1.25	(-1)1.73	(+2)4.23	(+1)7.26	(+3)3.20	(+4)2.51	(+1)5.62	(+1)6.66
10	(+1)1.37	(+1)2.02	(+1)4.13	(-1)8.86	(+3)2.17	(+2)3.72	(+5)3.19	(+6)2.50	(+2)1.14	(+1)6.67
11	(+1)8.67	(+2)1.28	(+2)2.60	(+4)1.28	(+4)1.28	(+3)2.20	(+8)2.67	(+9)2.09	(+2)1.11	(+1)5.25
(a) The weights are given in scientific notation, the power of ten being shown in parentheses. (b) The first column (σ = 1) refers to the non-standardized grid, the second column refers to the grid standardized by means of the middle root q_(n+1)/2, and the third column refers to the grid standardized by means of the central point of the interval q_center = ¹⁄₂. (c) The first column refers to the grid standardized by means of the central point of the interval q_center = ¹⁄₂, which yields σ = 1 by definition. The second column refers to the grid standardized by means of the middle root q_(n+1)/2. (d) Non-standardized grid.

10. Evenly spaced quadrature: the extended or composite trapezoidal rule

The definite integral of a function f(q) over some interval [a, b] can be approximated by the trapezoidal rule (also known as the trapezoid rule or trapezium rule, see left side of Figure 10.1), which estimates the area under the curve in the interval [a, b] by a right trapezoid with vertical bases f(a) and f(b) and horizontal height h = b − a:

b ∫ a f(q)dq ≈ b − a 2 [ f(a) + f(b) ]

(10.1)

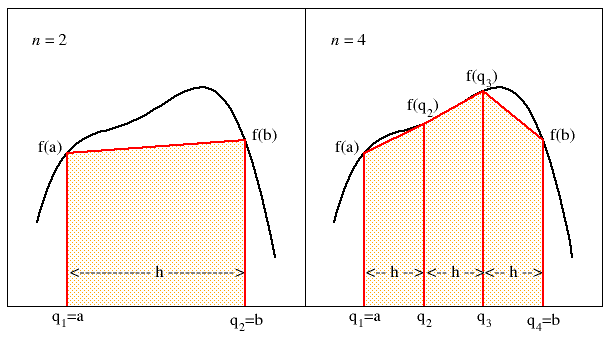Figure 10.1: Trapezoidal rule (on the left) and 4-point closed extended trapezoidal rule (on the right).

As shown in the right side of Figure 10.1, a better approxination is obtained by dividing the interval into a number of subintervals of equal length. Then the trapezoidal rule is used to estimate the area under the curve in each subinterval, and the results for all subintervals are summed together. For n equispaced points, using the trapezoidal rule (n - 1) times and adding the results gives the "extended" trapezoidal rule:

b = q_n ∫ a = q₁ f(q) dq = n−1 ∑ i=1 q_i+1 ∫ q_i f(q) dq ≈ 1 2 n−1 ∑ i=1 (q_i+1 − q_i) (f_i + f_i+1) = h ( 1 2 f₁ + n−1 ∑ i=2 f_i + 1 2 f_n ) = n ∑ i=1 w_i f(q_i)

(10.2)

where the evaluation points, q_i, and the associated weights, w_i, are defined by

q_i = a + (i − 1) h (∀ i = 1, 2, ..., n)
w₁ = w_n = h / 2 and w₂ = w₃ = … = w_{n − 1} = h	(10.3)
h = b − a / n − 1

and f(q_i) ≡ f_i, f(a) ≡ f(q₁) ≡ f₁, f(b) ≡ f(q_n) ≡ f_n. This n-point closed extended trapezoidal rule belongs to a large family of numerical integration techniques for equispaced points, known as Newton-Cotes formulas. The term "closed" means that points a and b are included in the formula, whereas "open" formulas consider only points belonging to the interval [q₂, q_n−1] and "semi-open" formulas refer to points in the intervals [q₁, q_n−1] and [q₂, q_n]. For instance, if f(q) has a singularity at the endpoint q_n, the last integral in the summation of Eq. (10.2) can be approximated by:

q_n ∫ q_n−1 f(q) dq ≈ h f(q_n−1) ≡ h f_n−1

(10.4)

and Eq. (10.2) yields the n-point semi-open trapezoidal formula:

b = q_n ∫ a = q₁ f(q) dq ≈ h ( 1 2 f₁ + n−2 ∑ i=2 f_i + 3 2 f_n−1 )

(10.5)

which is de facto reduced to a (n − 1)-point formula. In order that the semi-open trapezoidal formula has n evaluation points effectively, a (n + 1)-point formula is needed with n equal intervals of length h = (b − a)/n, and weights w₁ = ¹⁄₂h, w₂ = w₃ = … = w_n−1 = h, and w_n = ³⁄₂h.

The n-point trapezoid rule integrates exactly all spherical harmonics of degree L = n − 1 or less, so that, for a given L, a number of n = (L + 1) integration points is needed.

The following paragraphs describe two main applications of the extended trapezoidal rule in PAMoC.

φ quadrature over the interval [0, 2π]. In the case of explicit user request to estimate the angular integral by the two-term (N_θ, N_φ) product formula ("intgrid 8 | 9 | 10" and "intgrid -mmmlll"), PAMoC uses the closed extended trapezoidal rule for the φ quadrature over the interval [0, 2π]. In this case, using (n + 1) equispaced points, from φ₁ = 0 to φ_n+1 = 2π with step-size h = 2π/n, and observing that f(0) = f(2π), we have:

2π ∫ 0 f(φ)dφ ≈ 2π n n ∑ i=1 f(φ_i),

(10.6)

where φ_i = (i − 1) (2π/n), ∀ i = 1, 2, …, n.

Radial integral. The trapezoidal rule is also used by PAMoC to estimate the radial integral (2.11), in conjunction with a suitable variable transformation to map the improper interval [r₀, ∞] of the radial coordinate r to the finite interval [a, b] of the variable q. Two transformations were just designed by Handy[3Murray, C. W.; Handy, N. C.; Laming, G. J.
Mol. Phys. 1993, 78, 997-1014.] and Knowles.[8Mura, M. E.; Knowles, P. J.
J. Chem. Phys. 1996, 104, 9848-9858.] for use in combination with the composite trapezoid rule. However, also Becke, Ahlrichs, and Gill-Chien transformations can be used as well.

If the radial coordinate r is expressed as a function of the variable q ∈ [a, b], i.e. r ≡ r(q), so that dr = r'(q) dq, then the radial integral (2.11) can be solved by substitution, yielding

+∞ ∫ 0 r² g(r) dr = b ∫ a r²(q) r'(q) g(r) dq ≡ b ∫ a G(q) dq

(10.7)

where the integrand is now given by G(q) = r²(q) r'(q) g(r). Applying the quadrature rule (10.2), yields

b ∫ a G(q) dq ≈ n ∑ i=1 w_i G(q_i) = n ∑ i=1 ν_i g(r_i)

(10.8)

where the ν_i are the transformed weights

ν_i = r²(q_i) r'(q_i) w_i

(10.9)

and the q_i and w_i have expressions like those of eq. (10.3).

Handy's grid. In 1993, Murray, Handy and Laming introduced the transformation:[3Murray, C. W.; Handy, N. C.; Laming, G. J.
Mol. Phys. 1993, 78, 997-1014.]

r = r₀ + R q^m (1 − q)^m ⇒ dr = m R q^m−1 (1 − q)^m+1 dq

(10.10)

The displacement of the origin from 0 to r₀ was not considered in the original paper, but has been added here for completeness. At the origin is q = 0, r(0) = r₀, r'(0) = 0, and G(0) = r²(0) r'(0) g[r(0)] = 0. On the other hand, as q → 1⁻, the sample points eventually tend toward infinity and G(q) becomes singular. For this reason, a semi-open extended trapezoidal rule is needed, and the variable q is conveniently sampled over (n + 2) equispaced points, according to the relationship

q_i = i h = i n + 1 ∀ i = 0, 1, 2, …, n, n+1

(10.11)

which satisfies the conditions q₀ = 0 and q_n+1 = 1. However the quadrature rule comprises only n points q_i (i = 1, 2, …, n), because the first point does not contribute to the summation as r'(q₀) and G(q₀) are always zero (for m > 1), and the endpoint is discarded, since G(q_n+1) is singular. So, the n evaluation points r_i and the associated transformed weights ν_i, which define the Handy grid, are

r_i = r₀ + R q_i^m / (1 − q_i)^m = r₀ + R i^m / (n − i + 1)^m
ν_i = w_i m / q_i (1 − q_i) (r_i − r₀) r_i² = w_i m (n + 1)² / i (n − i + 1) (r_i − r₀) r_i² ∀ i = 1, 2, …, n	(10.12)
q_i = i h, w₁ = w₂ = … = w_{n − 1} = h, w_n = 3 / 2 h, h = 1 / n + 1, m ≥ 2

At the grid mid-point, if n is odd, we have i = (n + 1)/2, q_{(n + 1)/2} = ¹⁄₂, and r_{(n + 1)/2} - r₀ / R = 1, which states that the Handy grid is standardized, according to the definition by Gill and Chien.[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.]

If m is equal to one, then r'(q₀) is not null. Indeed in this case r'(q) = R/(1 − q), r'(q₀) = R, and ν₀ is proportional to R r₀². Then, if r₀ is not null, an (n+1)-point semi-open extended trapezoid quadrature provides the n evaluation points q_i = (i − 1)h ∀ i = 1, 2, …, n, and the associated weights w₁ = ¹⁄₂ h, w₂ = w₃ = … = w_{n − 1} = h, w_n = ³⁄₂ h, with h = ¹⁄_n.

Gill and Chien showed[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.] that the Handy grid is exact if G(q) = m R³ q^3m−1 / (1 − q)^3m+1 g[r(q)] equals L(q), a continuous function that is linear between the roots q_i = i/(n + 1) and which vanishes at q = 0 and q = 1. This implies, for r₀ = 0,

g(r) = ^{^m}√R m r^(3m−1)/m ( ^{^m}√R + ^{^m}√r )² L ( ^{^m}√r ^{^m}√R + ^{^m}√r) )

(10.13)

In general, such g(r) possess a 1/r^(3m−2)/m singularity at the origin and decay as 1/r^(3m+1)/m for large r.[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.]

In PAMoC, radial integration by the semi-open extended trapezoidal rule, combined with the Handy grid with m = 2, can be selected by the keyword "radrule 73". This is the only option available in all versions of PAMoC before 2013.

Knowles' grid. In 1996, Mura and Knowles introduced the transformation:[8Mura, M. E.; Knowles, P. J.
J. Chem. Phys. 1996, 104, 9848-9858.]

r = r₀ − R ln (1 − q^k) ⇒ dr = k R q^k−1 1 − q^k dq

(10.14)

which, at both the origin and the endpoint, behaves as the Handy transformation. Therefore, sampling q over (n + 2) equispaced points according to eq. (10.11), leads to a (n + 2)-point semi-open quadrature formula, which de facto reduces to a n-point formula like (10.10), whose evaluation points and weights define the Knowles grid:

r_i = r₀ − R ln (1 − q_i^k)
ν_i = k R q_i^k−1 / 1 − q_i^k w_i r_i² ∀ i = 1, 2, …, n	(10.15)
q_i = i h, w₁ = w₂ = … = w_{n − 1} = h, w_n = 3 / 2 h, h = 1 / n + 1, k ≥ 2

For i = n + 1 (i.e. q_n+1 = 1) both r_i and ν_i are singular, so that the last evaluation point is discarded and the weight of the n-th point is multiplied by ³⁄₂. For i = 0 (i.e. q₀ = 0) it is r_i = r₀ and ν₀ = 0, so that the first evaluation point, q₀, doesn't contribute to the integral and therefore has been excluded from the grid. However, if k = 1, q₀ can be excluded from the grid only if r₀ = 0, as ν₀ is proportional to R r₀². So, as in the case of the Handy grid for m = 1, if k = 1 and r₀ is not null, an (n+1)-point semi-open extended trapezoid quadrature provides the n evaluation points q_i = (i − 1)h ∀ i = 1, 2, …, n, and the associated weights w₁ = ¹⁄₂ h, w₂ = w₃ = … = w_{n − 1} = h, w_n = ³⁄₂ h, with h = ¹⁄_n.

At the grid mid-point, if n is odd, we have i = (n + 1)/2, q_{(n + 1)/2} = ¹⁄₂, and r_{(n + 1)/2} - r₀ / R = ln 2^k / 2^k − 1 = 1 / σ_k. Here, σ_k = ln⁻¹ 2^k / 2^k − 1 is the standardization factor for the Knowles grid (cf § 2.3.4). In particular, we have σ₁ = ln⁻¹(2) = 1.442695, σ₂ = ln⁻¹(⁴⁄₃) = 3.476059, σ₃ = ln⁻¹(⁸⁄₇) = 7.488876, and σ₄ = ln⁻¹(¹⁶⁄₁₅) = 15.494622, for k = 1, 2, 3, and 4, respectively. Mura and Knowles called the transformation (10.14) the “Log-k” transformation. They found that the Log3 grid was the most efficient in integrating the atomic density and common exchange correlation functionals, with scaling parameter values of R = 5.0 (for H-He, B-Ne, Al-Zr, and Sc-Zn) and R = 7.0 (for Li-Be, Na-Mg, and K-Ca), which are in the range of the value σ₃ = 7.488876 adopted in PAMoC.

For r₀ = 0 and R = 1, the Knowles grid is exact if G(q) = k q^k−1 ln²(1 − q^k) / 1 − q^k g[r(q)] equals L(q), which implies

g(r) = exp(−r) k r² [1 − exp(−r)]^(k−1)/k L( ^{^k}√1 − exp(−r) )

(10.16)

In general, such g(r) possess a 1/r^(3k−2)/k singularity at the origin and decay exponentially.[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.]

In PAMoC, radial integration by the semi-open extended trapezoidal rule, combined with Knowles' Log3 grid, is selected by the keyword "radrule 72".

Gill and Chien transformation of the radial coordinate. The (n+1)-point semi-open extended trapezoid rule can be used in combination with the transformation (9.2), introduced by Gill and Chien,[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003,24, 732-740.] to define the grid:

r_i = r₀ − R ln q_i
ν_i = − R r_i² w_i / q_i ∀ i = 1, 2, …, n	(10.17)
q_i = (n − i + 1) h, h = 1 / n and w₁ = 1 / 2 h, w₂ = w₃ = … = w_{n − 1} = h, w_n = 3 / 2 h, r₀ ≠ 0.

Indeed, this transformation of the radial coordinate has been thought to be used in conjunction with the Gauss-Gill “log-squared” quadrature rule (9.1).[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003,24, 732-740.] However, nothing prevents to apply it to a set of evenly spaced points.

For i = n + 1 (i.e. q_n+1 = 0) both r_i and ν_i are singular, so that the (n+1)-th evaluation point is discarded and the weight of the n-th point is multiplied by ³⁄₂. For i = 1 (i.e. q₁ = 1) it is r₁ = r₀ and ν₁ is proportional to R r₀², so that the first evaluation point contributes to the integral only if r₀ ≠ 0. Otherwise, if r₀ = 0, the n evaluation points may be calculates as q_i = (n − i + 1)/(n + 1) ∀ i = 1, 2, …, n, and the associated weights as w₁ = w₂ = … = w_n−1 = h, w_n = ³⁄₂ h, with h = 1/(n + 1).

At the center of the interval, it is q = ¹⁄₂, i = ⁽ⁿ⁺²⁾⁄₂, and r = r₀ + R ln 2, so that the standardization factor can be defined as either σ_PAMoC = 1/ln 2 = 1.4427 or σ_Gill-Chien = 1/q_(n+2)/2. The two values are rather close, depending on n, and become closer and closer as n increases. In PAMoC, grid (10.17) can be used for radial integration through the keyword "radrule 71".

Becke's grid. In Becke's transformation of the radial coordinate,[2Becke, A. D.
J. Chem. Phys. 1988, 88, 2547-2553.] defined by eq. (8.4), the variable q is defined in the interval [−1, +1], so that r = r₀ at q = −1, and is singular at q = 1. So, an (n+1)-point semi-open extended trapezoid rule can be used to obtain the grid:

r_i = r₀ + R 1 + q_i / 1 − q_i = r₀ + R i − 1 / n − i + 1
ν_i = 2 R r_i² / (1 − q_i)² w_i ∀ i = 1, 2, …, n	(10.18)
q_i = 2 i − n − 2 / n, h = 2 / n and w₁ = 1 / 2 h, w₂ = w₃ = … = w_{n − 1} = h, w_n = 3 / 2 h, r₀ ≠ 0

For i = n + 1 (i.e. q_n+1 = 1) both r_i and ν_i are singular, so that the (n+1)-th evaluation point is discarded and the weight of the n-th point is multiplied by ³⁄₂. For i = 1 (i.e. q₁ = − 1) it is r₁ = r₀ and ν₁ is proportional to R r₀², so that the first evaluation point contributes to the integral only if r₀ ≠ 0. Otherwise, if r₀ = 0, the n evaluation points may be calculates as q_i = (2 i − n − 1)/(n + 1) ∀ i = 1, 2, …, n, and the associated weights as w₁ = w₂ = … = w_n−1 = h, w_n = ³⁄₂ h, with h = 2/(n + 1).

At the center of the interval, it is q = 0, i = (n+2)/2, and r = r₀ + R, so that the standardization factor is equal one and the grid doesn't need to be standardized. In PAMoC, grid (10.18) can be used for radial integration through the keyword "radrule 75".

Ahlrichs' grid. In Ahlrichs' transformation,[7Treutler, O.; Ahlrichs, R.
J. Chem. Phys. 1995, 102, 346-354.] defined by eq. (8.8), the variable q is defined in the interval [−1, +1], so that r = r₀ at q = −1, and is singular at q = 1. So, an (n+2)-point semi-open extended trapezoid rule can be used to obtain the grid:

r_i = r₀ − R / ln 2 (1 + q_i)^α ln 1 − q_i / 2
ν_i = r_i² R / ln 2 (1 + q_i)^α−1 ( 1 + q_i / 1 − q_i − α ln 1 − q_i / 2) w_i ∀ i = 1, 2, …, n	(10.19)
q_i = 2 i − n − 1 / n + 1, h = 2 / n + 1 and w₁ = w₂ = … = w_{n − 1} = h, w_n = 3 / 2 h

For i = n + 1 (i.e. q_n+1 = 1) both r_i and ν_i are singular, so that the (n+2)-th evaluation point is discarded and the weight of the n-th point is multiplied by ³⁄₂. For i = 0 (i.e. q₀ = − 1) it is r_i = r₀ and ν₀ = 0, so that the first evaluation point, q₀, doesn't contribute to the integral ond therefore has been excluded from the grid. At the center of the interval, it is q = 0, i = (n+1)/2, and r = r₀ + R, so that the standardization factor is equal one and the grid doesn't need to be standardized. In PAMoC, grid (10.19) can be used for radial integration through the keyword "radrule 76".

Modified Handy's grid for finite intervals of the radial coordinate r. Figure 10.4 shows that Handy's grid comprises a number of points which are very far from the nucleus, and which probably contribute very little to the integral of typically exponentially (or Gaussian) decaying integrands. Such points can, of course, be systematically neglected within computer programs by dynamic pruning of the grid, which is reduced by about 20% of its original size.[3Murray, C. W.; Handy, N. C.; Laming, G. J.
Mol. Phys. 1993, 78, 997-1014., 4Gill, P. M. W.; Johnson, B. G.; Pople, J. A.
Chem. Phys. Lett. 1993, 209, 506-512., 10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003, 24, 732-740.] On this line, PAMoC truncates the summation in the right hand side of eq. (10.10) at a value N_r < n such that q_{N_r} ≤ r_max, where r_max is large enough (usually 10 bohr) to be a good approximation to infinity. However. Mura and Knowles pointed out that it is preferable to use more appropriate grids from the outset[8Mura, M. E.; Knowles, P. J.
J. Chem. Phys. 1996, 104, 9848-9858.] and indeed the Knowles grid is relatively compact, as shown in Figure 10.4. Therefore, a modified form of the Murray, Handy and Laming transformation[3Murray, C. W.; Handy, N. C.; Laming, G. J.
Mol. Phys. 1993, 78, 997-1014.] is made available in PAMoC to map the interval [r₀, r_max] to the interval [0, 1]:

r(q) = r₀ + (r_max − r₀) q^m 1 + (r_max − r₀ − 2^m)(1 − q)^m ⇒
dr = m (r_max − r₀) [1 + (r_max − r₀ − 2^m)(1 − q)^m−1] q^m−1 [1 + (r_max − r₀ − 2^m) (1 − q)^m]² dq

(10.20)

which provides a distribution of the sample points concentrated at the origin r₀ and with the furthest points at a distance from the nucleus which does not exceed r_max. At the origin and for m ≥ 2, it is q = 0, r(0) = r₀, r'(0) = 0, and G(0) = r²(0) r'(0) g[r(0)] = 0. At the endpoint it is q = 1, r(1) = r_max, r'(1) = m (r_max − r₀), and G(1) = r²(1) r'(1) g[r(1)] = m r_max² (r_max − r₀) g(r_max). At the grid midpoint it is q = ¹⁄₂ and r(¹⁄₂) = 1, so that the grid is standardized by construction. Sampling q over n equispaced points, i.e. q = ⁽ⁱ⁻¹⁾⁄_(n−1) ∀ i = 1, 2, …, n, leads to a n-point closed quadrature formula, whose leading term is null because r'(0) and then ν₁ are zero by definition. Thus, the change of variable of eq. (10.20) coupled with the integration by substitution and with the trapezoidal rule, yields:

r_max ∫ r₀ r² g(r) dr = 1 ∫ 0 r²(q) r'(q) g[r(q)] dq ≡ 1 ∫ 0 G(q) dq ≈
1 n − 1 ( 1 2 G₁ + n−1 ∑ i=2 G_i + 1 2 G_n ) = n ∑ i=1 w_i G_i = n ∑ i=1 ν_i g(r_i)

(10.21)

The evalution points r_i and their associated weights ν_i and w_i define the modified Handy grid for the finite interval [r₀, r_max]:

r_i = r₀ + (r_max − r₀) q_i^m / 1 + (r_max − r₀ − 2^m)(1 − q_i)^m
ν_i = m (r_max − r₀) w_i r_i² [1 + (r_max − r₀ − 2^m)(1 − q_i)^m−1] q_i^m−1 / [1 + (r_max − r₀ − 2^m) (1 − q_i)^m]² ∀ i = 1, 2, ..., n	(10.22)
q_i = (i − 1) h, w₁ = w_n = 1 / 2 h, w₂ = w₃ = … = w_{n − 1} = h, h = 1 / n − 1, m ≥ 2

If m is equal to one, then r'(q₀) is not null and ν₁ is proportional to (r_max − r₀) r₀² / (r_max − r₀ − 1). Then, if r₀ is not null, an n-point closed extended trapezoid quadrature provides the n evaluation points q_i = (i − 1)h ∀ i = 1, 2, …, n, and the associated weights w₁ = w_n = ¹⁄₂ h, w₂ = w₃ = … = w_n−1 = h, h = 1/(n − 1), m = 1, r₀ ≠ 0.

This grid is a good approximation for the integral of a radial function which changes rapidly in proximity of the origin and smootly vanishes at large distances. It is available in PAMoC through the keyword "radrule 74".

Linear grid for finite intervals of the radial coordinate r. For sake of completeness, is worth noting that if the radial coordinate r ∈ [r₀, r_max] is given by evenly spaced points, then the corresponding grid is:

r_i = r₀ + q_i
ν_i = w_i r_i² ∀ i = 1, 2, …, n	(10.23)
q_i = (i − 1) h, w₁ = w_n = 1 / 2 h, w₂ = w₃ = … = w_{n − 1} = h, and h = r_max − r₀ / n − 1

Such a grid provides sample points equally spaced from the origin r₀ to the furthest point at a distance r_max from the origin. At the origin it is q₁ = 0, r₁ = r₀, r'₁ = 1, and G₁ = r₀² g(r₀). At the endpoint it is q_n = r_max − r₀, r_n = r_max, r_n' = 1, and G_n = r_max² g(r_max). At the grid midpoint it is q_(n+1)/2 = r_max − r₀, and r_(n+1)/2 = (r₀ + r_max)/2, so that the grid is not standardized.

It goes without saying that this is the worst grid that can be used for the radial quadrature. However PAMoC makes it available to masochists through keyword "radrule 77".

In order to compare the roots and weights from various transformations of the radial coordinate, coupled with the extended trapezoid quadrature scheme, the roots and weights for the 11-point Gill-Chien, Knowles, Handy, Becke, Ahlrichs, and linear grids are listed in Tables 10.2 and 10.3, respectively.

**Table 10.2.** − Evaluation Points (*r_i*) of Extended Trapezoid Quadrature over Equispaced Points (*q_i*), combined with different Transformations, r = r(q), of the Radial Coordinate.^(a)
	Gill-Chien and Knowles' Log1^(b)		Knowles' Log3^(b)
i	σ = 1	σ = 1.4427	σ = 1	σ = 7.4889	Handy^(c)	modified Handy^(c)	Becke^(c)	Ahlrichs^(c)	Linear^(d)
1	0.0870	0.1255	0.0006	0.0043	0.0083	0.0139	0.0909	0.0428	0.9091
2	0.1823	0.2630	0.0046	0.0348	0.0400	0.0659	0.2000	0.1361	1.8182
3	0.2877	0.4150	0.0157	0.1179	0.1111	0.1782	0.3333	0.2738	2.7273
4	0.4055	0.5850	0.0377	0.2826	0.2500	0.3855	0.5000	0.4586	3.6364
5	0.5390	0.7776	0.0751	0.5623	0.5102	0.7418	0.7143	0.6970	4.5455
6	0.6931	1.0000	0.1335	1.0000	1.0000	1.3284	1.0000	1.0000	5.4545
7	0.8755	1.2630	0.2213	1.6570	1.9600	2.2581	1.4000	1.3854	6.3636
8	1.0986	1.5850	0.3514	2.6316	4.0000	3.6571	2.0000	1.8836	7.2727
9	1.3863	2.0000	0.5480	4.1036	9.0000	5.5862	3.0000	2.5508	8.1818
10	1.7918	2.5850	0.8644	6.4735	25.0000	7.8740	5.0000	3.5121	9.0909
11	2.4849	3.5850	1.4708	11.0145	121.0000	10.0000	11.0000	5.1574	10.0000
(a) R = 1, r₀ = 0, and r_max = 10. (b) Both standardized (σ = 1.4427) and non-standardized (σ = 1) grids are reported. (c) This grid is standardized by construction. (d) Non-standardized grid.

**Table 10.3.** − Weights^(a) (*ν_i*) of Extended Trapezoid Quadrature over Equispaced Points (*q_i*), combined with different Transformations, r = r(q), of the Radial Coordinate.^(b)
	Gill-Chien and Knowles' Log1^(c)		Knowles' Log3^(c)
i	σ = 1	σ = 1.4427	σ = 1	σ = 7.4889	Handy^(d)	modified Handy^(d)	Becke^(d)	Ahlrichs^(d)	Linear^(e)
1	(-4)6.88	(-3)2.07	0	(-7)2.4	(-6)1.23	(-6)5.78	(-4)8.20	(-4)1.29	(-1)7.51
2	(-3)3.32	(-3)9.98	(-7)1.5	(-5)6.31	(-5)7.68	(-4)3.37	(-3)4.80	(-3)2.14	(+0)3.01
3	(-3)9.20	(-2)2.76	(-6)3.94	(-3)1.65	(-3)1.22	(-3)4.85	(-2)1.65	(-2)1.20	(+0)6.76
4	(-2)2.06	(-2)6.17	(-5)4.11	(-2)1.73	(-2)1.17	(-2)4.03	(-2)4.69	(-2)4.42	(+1)1.20
5	(-2)4.15	(-1)1.25	(-4)2.64	(-1)1.11	(-2)9.11	(-1)2.51	(-1)1.25	(-1)1.30	(+1)1.88
6	(-2)8.01	(-1)2.40	(-3)1.27	(-1)5.35	(-1)6.67	(+0)1.30	(-1)3.33	(-1)3.40	(+1)2.70
7	(-1)1.53	(-1)4.60	(-3)5.20	(+0)2.18	(+0)5.16	(+0)5.84	(-1)9.41	(-1)8.35	(+1)3.68
8	(-1)3.02	(-1)9.06	(-2)1.95	(+0)8.19	(+1)4.80	(+1)2.23	(+0)3.00	(+0)2.02	(+1)4.81
9	(-1)6.41	(+0)1.92	(-2)7.30	(+1)3.07	(+2)6.48	(+1)6.76	(+1)1.20	(+0)5.10	(+1)6.09
10	(+0)1.61	(+0)4.82	(-1)3.08	(+2)1.29	(+4)1.88	(+2)1.44	(+1)7.50	(+1)1.47	(+1)7.51
11	(+0)9.26	(+1)2.78	(+0)2.97	(+3)1.25	(+6)5.80	(+1)9.09	(+3)2.18	(+1)9.40	(+1)4.55
(a) The weights are given in scientific notation, the power of ten being shown in parentheses. (b) R = 1, r₀ = 0, and r_max = 10. (c) Both standardized (σ = 1.4427) and non-standardized (σ = 1) grids are reported. (d) This grid is standardized by construction. (e) Non-standardized grid.

The 11-point grids of Table 10.2 are illustrated in Figure 10.4. The 11-point Gill-Chien and Knowles' Log1 grids share the same roots (and weights). The only difference between them is that the former gives r_i values which increase as q_i values decrease, whereas the latter gives r_i values which increase with q_i values. The effect of standardization is to increase the resolution. This effect is clearly shown in Figure 10.4 for the Gill-Chien and Knowles grids, which, together with the linear, grid are not standardized by construction. Standardization ensures that the curves coincide at the middle root (r₁ = 1), but the Handy, Knowles and Becke grids extend further out, and the Ahlrichs and Knowles grids extend further in than the others. The Gill-Chien grid has the narrowest range of the seven. In all cases, resolution increases with the number of roots n.

**Figure 10.4:** Transformations of the radial coordinate r = r(q) using a set of n equally spaced points, *q_i*, which are suitable for the extended trapezoid quadrature rule (n = 11, r₀ = 0, and *r_max* = 10). (a) Gill-Chien transformation (black circles, eq. 10.15x, open circles refer to the non-standardized grid with σ = 1, full circles refer to the standardized grid with σ = 1.4427). (b) Knowles' Log1 grid (blue squares, eq. 10.13 with k = 1, open squares refer to the non-standardized grid with σ = 1, full squares refer to the standardized grid with σ = 1.4427). (c) Knowles' Log3 grid (orange squares, eq. 10.13 with k = 3, open squares refer to the non-standardized grid with σ = 1, full squares refer to the standardized grid with σ = 7.4889). (d) Handy grid (violet right triangles, eq. 10.7 with m = 2, the grid is standardized by construction). (e) modified Handy grid for finite intervals of r (violet left triangles, eq. 10.16 with m = 2 and *r_max* = 10, the grid is standardized by construction). (f) Becke's grid (dark green up triangles, eq. 10.15y, the grid is standardized by construction). (g) Ahlrichs' grid (magenta down triangles, eq. 10.15z, the grid is standardized by construction). (h) Linear grid for finite intervals of r (red stars, eq. 10.19 with *r_max* = 10, the grid is not standardized).

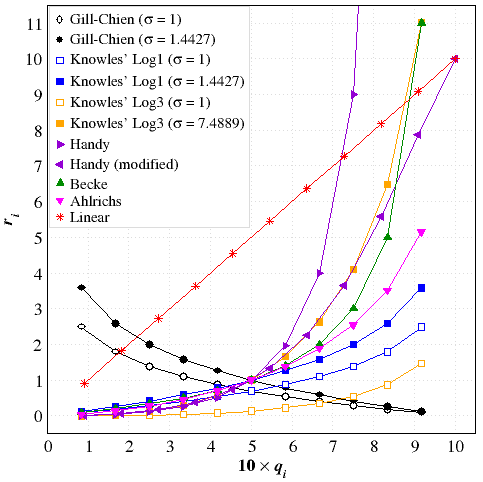
Euler-Maclaurin quadrature. The extended trapezoid quadrature is closely related to the Euler-Maclaurin summation formula, which is an important tool in numerical analysis to estimate sums or integrals of functions. For an integral in the interval [a, b] and a step length h = (b − a) / (n − 1), it takes the form:[16Smith, F. J.
Numer. Math. 1965, 7, 406-411., 17Graham, R. L.; Knuth, D. E.; Patashnik, O.
"Concrete Mathematics",
Second Edition, Addison-Wesley Publishing Company, Inc., 1994, eq. (9.67), p. 469.]

b = q_n ∫ a = q₁ f(q) dq = h ( 1 2 f₁ + n−1 ∑ i=2 f_i + 1 2 f_n ) − m ∑ k=1 h^2k B_2k (2k)! [ f^(2k−1)(b) − f^(2k−1)(a) ] + E_m(f)

(10.24)

where f(q) and its derivatives are continuous in [a, b] and q_i = a + h (i − 1). The remainder term E_m(f) has the expression:

E_m(f) = (a − b) h^2m+2 B_2m+2 (2m+2)! f^(2m+2)(ξ)

(10.25)

where ξ is some number in [a, b]. The remainder is often small and, in particular, it is zero if f^(2m+2)(q) = 0. The numbers B_j that appear in eqs (10.24) and (10.25) are Bernoulli numbers (B₀ = 1, B₁ = −¹⁄₂, B₂ = ¹⁄₆, B₄ = −¹⁄₃₀, B₆ = ¹⁄₄₂, B₈ = −¹⁄₃₀, ... ; B₃ = B₅ = B₇ = B₉ = ... = 0). The formula (10.24) is identical with the n-point closed extended trapezoidal rule (10.2) but with an expansion of the error term which is in general an asymptotic series.

If f(q) is the integrand of a radial integral, f(q) and its derivatives vanish at the origin a = q₀ = 0 and tend to zero at large distances, as b = q_n → ∞. Under these conditions, eq. (10.24) is often written as

∞ ∫ 0 f(q) dq = h n ∑ i=1 f_i

(10.26)

which is a simplified form of the trapezoidal rule.

11. Tests of radial grid accuracies

Gill and Chien warned about the opportunity “of selecting specific numerical examples to illustrate quadrature accuracy […], for one can always select examples to make a given scheme look as good, or as bad, as one wishes.”[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003,24, 732-740.] However, taking into account their advice, and mimicking their work, it is worth examining a few example tests, “not because they are conclusive, but because they are interesting.”[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003,24, 732-740.]

The radial functions reported in the first column of Table 11.2 are used to illustrate grid accuracy.[10Gill, P. M. W.; Chien, S.-H.
J. Comput. Chem. 2003,24, 732-740.] If the radial function g(r) is a Gaussian with unit exponent, Table 11.2 reveals that the grids may be ranked as

Handy < modified Handy < Knowles' Log3 < Becke ≈ Linear < Gill-Chien < Ahlrichs

Adding a second, tighter Gaussian, worsens the linear grid accuracy, yielding the ranking

Linear ≪ Handy < modified Handy < Becke ≈ Knowles' Log3 < Gill-Chien < Ahlrichs

Adding a third, even tighter Gaussian to g(r), leads to deterioration in all grid accuracies to yield

If the same test is done using an exponential function with unit exponent, the grids are ranked as

Ahlrichs < Gill-Chien < linear < Becke ≈ Knowles' Log3 ≈ modified Handy < Handy

Adding one and two exponential functions with exponent increasingly higher makes the linear grid accuracy the worst of all and leaves the ranking of the remaining ones unchanged.

Linear ≪ Knowles' Log3 ≈ Handy ≈ modified Handy < Ahlrichs ≈ Becke ≈ Gill-Chien

When the grids of Tables 10.2 and 10.3 are used to estimate the slowly converging radial integral of the function 1/(1 + r⁴) the results shown in the final row of Table 11.2 are obtained, with the grid ranking

Gill-Chien < Ahlrichs ≈ modified Handy ≈ linear < Knowles' Log3 < Handy < Becke

favoring the grids which sample the integrand at large r.

**Table 11.1.** − Functions used to test radial quadrature rules.
i	g(r)
1	exp(−r²)
2	∑_j=0,1 10^j exp(−10^j r²)
3	∑_j=0,1,2 10^j exp(−10^j r²)
4	exp(−r)
5	∑_j=0,1 10^2j exp(−10^j r)
6	∑_j=0,1,2 10^2j exp(−10^j r)
7	1/(1 + r⁴)

**Table 11.2.** − Accuracy^(a) of radial quadrature using the grids of Tables 10.2 and 10.3.
g(r)	Gill-Chien and Knowles' Log1 σ = 1.4427	Knowles' Log3 σ = 7.4889	Handy	modified Handy	Becke	Ahlrichs	Linear
1	4.1	3.3	2.0	2.9	3.5	5.3	3.5
2	4.0	3.7	2.3	2.8	3.6	5.3	0.6
3	3.1	2.3	2.4	2.4	3.1	3.0	0.5
4	1.4	2.5	2.8	2.5	2.5	1.2	2.3
5	1.4	2.5	2.8	2.5	2.6	1.3	1.0
6	1.3	2.4	2.8	2.5	2.2	1.3	1.0
7	0.8	1.5	2.1	1.0	2.2	1.0	1.1
(a) As suggested by Gill and Chien,[10Gill, P. M. W.; Chien, S.-H. J. Comput. Chem. 2003,24, 732-740.] the quality of a quadrature estimation (“Approx”) of an integral is compared with the exact value (“Exact”) using the equation Accuracy = −log₁₀ \| Approx / Exact − 1 \| The resulting values are essentially the number of correct digits in the quadrature result.

It is clear that, if r is null outside the interval [0,10], the Log1 grid should not be coupled with the Euler-Maclaurin quadrature because it covers less than half of the interval. On the other hand, the Handy grid should be discarded because two points (18%) fall outside the interval. Therefore the modified Handy grid and Knowles' Log3 grid remain as suitable choices for the Euler-Maclaurin radial quadrature.

**Table 11.3.** − Accuracy^(a) of radial quadrature using the grids of Tables 9.2 and 9.3.
	MultiExp^(b)			Knowles' Log3^(b)			Handy^(c)
i	σ = 1	σ = 1.1374	σ = 1.4427	σ = 1	σ = 13.4747	σ = 7.4889	σ = 1	σ = 1.9854	modified Handy^(d)	Linear^(d)
1	4.7	4.9	5.3	2.8	1.6	1.7	0.9	1.7	1.6	3.0
2	4.8	4.8	4.9	2.6	1.8	2.3	0.9	2.3	1.9	1.3
3	3.3	3.1	2.6	2.5	1.7	2.1	0.9	1.8	3.0	1.6
4	8.1	2.2	2.5	0.3	6.6	6.0	1.5	1.9	2.4	2.5
5	7.9	2.3	2.5	0.4	2.6	3.1	1.5	2.0	2.4	2.1
6	2.5	3.0	2.5	0.4	5.0	2.9	1.5	2.1	2.4	2.2
7	0.9	1.0	1.1	0.5	2.1	1.4	2.3	1.7	1.0	1.1
(a) See note (a) in Table 11.2 for definition of accuracy. (b-d) See the corresponding notes in Table 9.2.

**Table 11.4.** − Accuracy^(a) of radial quadrature using the grids of Tables 9.2 and 9.3.
	Gauss-Legendre Quadrature^(b)			2nd kind Chebyshev Quadrature^(b)
i	Becke	Ahlrichs	Linear	Becke	Ahlrichs	Linear
1	2.2	3.4	2.6	2.3	3.7	3.6
2	2.3	3.5	1.3	2.4	3.2	1.2
3	2.3	4.0	1.3	2.5	2.4	1.4
4	2.8	3.9	2.6	2.5	3.5	2.5
5	2.9	3.9	2.0	2.5	3.6	2.4
6	3.5	2.9	1.7	2.5	2.8	2.3
7	3.7	1.2	1.0	2.6	1.1	1.0
(a) See note (a) in Table 11.2 for definition of accuracy. (b-d) See the corresponding notes in Table 9.2.

Concluding Remarks

None of the quadrature schemes outlined above are perfect, and each can be criticized on both aesthetic and practical grounds.[11El-Sherbiny, A.; Poirier, R.A.
J. Comp. Chem. 2004, 25, 1378-1384.] One can say for sure that there is no absolute favorite radial quadrature scheme, which dominates others, so that is worth that programs for atomic quadratures have several for users to choose from.

The quadrature methods examined so far use grid points and weights that are known beforehand. Other schemes have been designed, in which points and weights are chosen dynamically as the integrand is explored.[12(a) Pérez-Jordá, J. M.; San-Fabián, E.; Moscardó, F.
Comp. Phys. Commun. 1992, 70, 271-284.
(b) Pérez-Jordá, J. M.; San-Fabián, E.
Comp. Phys. Commun. 1993, 77, 46-56.
(c) Pérez-Jordá, J. M.; Becke A. D.; San-Fabián, E.
J. Chem. Phys. 1994, 100, 6520-6534.; 13(a) Krack, M.; Köster, A. M.
J. Chem. Phys. 1998, 108, 3226-3234.
(b) Köster, A. M.; Flores-Moreno, R.; Reveles, J. U.
J. Chem. Phys. 2004, 121, 681-690.; 14 Gräfenstein, J.; Cremer, D.
J. Chem. Phys. 2007 127, 164113-7.; 15Kakhiani, K.; Tsereteli, K.; Tsereteli, P.
Computer Physics Communications 2009, 180, 256-268.]

References

"Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten"
Runge, C. Zeitschrift für Mathematik und Physik 1901, 46, 224-243.
"A multicenter numerical integration scheme for polyatomic molecules"
Becke, A. D. J. Chem. Phys. 1988, 88, 2547-2553.
"Quadrature schemes for integrals of density functional theory"
Murray, C. W.; Handy, N. C.; Laming, G. J. Mol. Phys. 1993, 78, 997-1014.
"A standard grid for density functional calculations"
Gill, P. M. W.; Johnson, B. G.; Pople, J. A. Chem. Phys. Lett. 1993, 209, 506-512.
(a) "Values of the nodes and weights of ninth to seventeenth order Gauss-Markov quadrature formulae invariant under
the octahedron group with inversion"

Lebedev, V.I. USSR Comp. Math. and Math. Phys. 1975, 15(1), 44-51. Zh. vychisl. Mat. mat. Fiz. 1975, 15(1), 48-54.
(b) "Quadratures on a sphere"

Lebedev, V.I. USSR Comp. Math. and Math. Phys. 1976, 16(2), 10-24. Zh. vychisl. Mat. mat. Fiz. 1976, 16(2), 293-306.
(c) "Spherical quadrature formulas exact to orders 25-29"

Lebedev, V.I. Siberian. Math. J. 1977, 18(1), 99-107. Sibirskii Matematicheskii Zhurnal 1977, 18(1), 132-142.
(d) "Quadrature formulas of orders 41, 47, and 53 for the sphere"

Lebedev, V. I.; Skorokhodov, A. L. Russian Acad. Sci. Dokl. Math. 1992, 45, 587-592.
(e) "A quadrature formula for the sphere of 59th algebraic order of accuracy"

Lebedev, V. I. Russian Acad. Sci. Dokl. Math. 1995, 50, 283-286.
(f) "A quadrature formula for the sphere of the 131-st algebraic order of accuracy"

Lebedev, V.I.; Laikov, D.N. Dokl. Math. 1999, 59, 477-481.
"An Investigation of the Performance of a Hybrid of Hartree-Fock and Density Functional Theory"
Gill, P.M.W.; Johnson, B.J.; Pople, J.A.; Frisch, M.J. Intern. J. Quantum Chem. Symp. 1992, 26, 319-331.
"Efficient molecular numerical integration schemes"
Treutler, O.; Ahlrichs, R. J. Chem. Phys. 1995, 102, 346-354.
"Improved radial grids for quadrature in molecular density-functional calculations"
Mura, M. E.; Knowles, P. J. J. Chem. Phys. 1996, 104, 9848-9858.
"Molecular integrals by numerical quadrature. I. Radial integration"
Lindh, R.; Malmqvist, P.-A.; Gagliardi, L. Theor. Chem. Acc. 2001, 106, 178-187.
"Radial Quadrature for Multiexponential Integrands"
Gill, P. M. W.; Chien, S.-H. J. Comput. Chem. 2003, 24, 732-740.
"An Evaluation of the Radial Part of Numerical Integration Commonly Used in DFT"
El-Sherbiny, A.; Poirier, R.A. J. Comp. Chem. 2004, 25, 1378-1384.
(a) "A simple, reliable and efficient scheme for automatic numerical integration"
Pérez-Jordá, J. M.; San-Fabián, E.; Moscardó, F. Comp. Phys. Commun. 1992, 70, 271-284.
(b) "A simple, efficient and more reliable scheme for automatic numerical integration"
Pérez-Jordá, J. M.; San-Fabián, E. Comp. Phys. Commun. 1993, 77, 46-56.
(c) "Automatic numerical integration techniques for polyatomic molecules"
Pérez-Jordá, J. M.; Becke A. D.; San-Fabián, E. J. Chem. Phys. 1994, 100, 6520-6534.
(a) "An adaptive numerical integrator for molecular integrals"

Krack, M.; Köster, A. M. J. Chem. Phys. 1998, 108, 3226-3234.
(b) "Efficient and reliable numerical integration of exchange-correlation energies and potentials"

Köster, A. M.; Flores-Moreno, R.; Reveles, J. U. J. Chem. Phys. 2004, 121, 681-690.
"Efficient density-functional theory integrations by locally augmented radial grids"
Gräfenstein, J.; Cremer, D. J. Chem. Phys. 2007 127, 164113-7.
"A program to generate a basis set adaptive radial quadrature grid for density functional theory"
Kakhiani, K.; Tsereteli, K.; Tsereteli, P. Computer Physics Communications 2009, 180, 256-268.
"The arrangement of atoms in crystals"
Bragg, W. L. Philos. Mag. 1920, 40, 169-189.
"Atomic Radii in Crystals"
Slater, J. C. J. Chem. Phys. 1964, 41, 3199-3204.
"Covalent radii revisited"
Cordero, B.; Gómez, V.; Platero-Prats, A. E.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S. Dalton Trans. 2008, 2832-2838.
"Atomic Shielding Constants"
Slater, J. C. Phys. Rev. 1930, 36, 57-64.
"Atomic Screening Constants from SCF Functions. II. Atoms with 37 to 86 Electrons"
Clementi, E.; Raimondi, D. L.; Reinhardt, W. P. J. Chem. Phys. 1967, 47, 1300-1307.
"A local projection method for the linear combination of atomic orbital implementation of density-functional theory"
Yang, W. J. Chem. Phys. 1991, 94, 1208-1214.
"Distributed Multipole Analysis: Stability for Large Basis Sets"
Stone, A. J. J. Chem. Theory Comput. 2005, 1, 1128-1132.
"Electronic Wave Functions. I. A General Method of Calculation for the Stationary States of Any Molecular System"
Boys, S. F. Proc. Roy. Soc. A 1950, 200, 542-554.
"Gaussian quadrature formulae for ∫₀¹−ln(x)f(x)dx"
Anderson, D.G. Math. Comp. 1965, 19, 477-481.
"Calculation of Gauss Quadrature Rules"
Golub, G.H.; Welsch, J.H. Math. Comp. 1969, 23, 221-230.
"SG-0: A Small Standard Grid for DFT Quadrature on Large Systems"
Chien, S.-H.; Gill, P. M. W. J. Comput. Chem. 2006, 27, 730-739.
"Algorithm 655: IQPACK, FORTRAN Subroutines for the Weights of Interpolatory Quadrature"
Elhay, Sylvan; Kautsky, Jaroslav ACM Transactions on Mathematical Software 1987, 13, 399-415.
"Quadrature methods based on the Euler-Maclaurin formula and on the Clenshaw-Curtis method of integration"
Smith, F. J. Numer. Math. 1965, 7, 406-411.
Graham, R. L.; Knuth, D. E.; Patashnik, O. "Concrete Mathematics", Second Edition, Addison-Wesley Publishing Company, Inc., 1994, eq. (9.67), p. 469.

Notes

Jacobian matrix. In mathematics, the Jacobian matrix (sometimes simply called "the Jacobian") is the matrix of all first-order partial derivatives of a vector-valued function. Suppose f : ℝⁿ → ℝ^m is a function which takes as input the vector x ∈ ℝⁿ and produces as output the vector f(x) ∈ ℝ^m. Then the Jacobian matrix J of f is an m×n matrix, usually defined and arranged as follows:

J = ∂ f ∂ x = ( ∂ f ∂ x₁ … ∂ f ∂ x_n ) =

∂f₁ / ∂x₁	…	∂f₁ / ∂x_n
⋮	⋱	⋮
∂f_m / ∂x₁	…	∂f_m / ∂x_n

(N1)

As a mnemonic, it is worth noting that across a row of the Jacobian matrix the numerators are the same and down a column the denominators are the same.

If m = n, the Jacobian matrix is a square matrix, and therefore admits a determinant, the Jacobian determinant of f.

If m = 1, f is a scalar-valued function of multiple variables, f(x₁,…,x_n), and the Jacobian matrix is reduced to a row vector of partial derivatives of f, i.e. the transpose of the gradient of f, ∇^†f (confusingly, often called "the Jacobian" as well).

The transpose of the Jacobian matrix can be viewed as the gradient of the transpose of the vector-valued function f, i.e. J^† = ∇f^†. Then, the Jacobian generalizes the gradient of a scalar-valued function of multiple variables, which itself generalizes the derivative of a scalar-valued function of a single variable. In other words, the Jacobian for a scalar-valued multivariate function is the gradient and that of a scalar-valued function of single variable is simply its derivative.

[Main source of this note: Wikipedia contributors. Jacobian matrix and determinant. Wikipedia, The Free Encyclopedia. Available at: https://en.wikipedia.org/w/index.php?title=Jacobian_matrix_and_determinant&oldid=834303707. Accessed April 13, 2018].

Methods of Numerical Integration.

1. - Numerical estimation of integrals

2. - Volume integral

2.1. - Partitioning into atomic subintegrals.

2.2. - Angular integral.

2.3. - Radial integral and transformations of the radial coordinate.

3. Lebedev angular quadrature

3. Gauss-Legendre quadrature

4. Gauss-Laguerre quadrature

5. Generalized Gauss-Laguerre quadrature

6. Gauss-Hermite quadrature

8. Gauss-Chebyshev quadrature of the second kind

9. Gauss-Gill quadrature

10. Evenly spaced quadrature: the extended or composite trapezoidal rule

11. Tests of radial grid accuracies

Concluding Remarks

References

Notes

Links