Proatoms, promolecules, and procrystals.
A tutorial.
Promolecule
“Molecular Surfaces from the Promolecule: A Comparison with
Hartree-Fock Ab Initio Electron Density Surfaces”
Mitchell, A. S.; Spackman, M. A. J. Comput. Chem. 2000,
21, 933-942.
The term promolecule, originally used by Hirshfeld and Rzotkiewicz,
[27 ... “Electrostatic binding in the first-row AH and A2
diatomic molecules”
Hirshfeld, F. L.; Rzotkiewicz, S. Mol. Phys. 1974,
27, 1319-1343.]
refers to a reference electron density consisting of overlapping,
spherically averaged, undeformed atoms prior to molecule formation.
It is equivalent to the independent atom model (IAM) in electron scattering,
and the spherical atom approximation in X-ray crystallography.
[…]
The properties of the promolecule are reasonably well understood, and
it is known to provide chemically sensible atomic radii,
[30 ... Gibbs, G. V.; Spackman, M. A.; Boisen, M. B. Am Mineral 1992, 77, 741.
31 ... Spackman, M. A.; Maslen, E. N. J Phys Chem 1986, 90, 2020.]
electrostatic binding energies,
[27 ... Hirshfeld, F. L.; Rzotkiewicz, S. Mol Phys 1974, 27, 1319.]
31 ... Spackman, M. A.; Maslen, E. N. J Phys Chem 1986, 90, 2020.
32 ... Trefry, M. G.; Maslen, E. N.; Spackman, M. A.
J Phys C: Solid State Phys 1987, 20, 19.]
atom–atom potentials,
[33 ... Spackman, M. A. J Chem Phys 1986, 85, 6579.]
diamagnetic shielding constants, and diamagnetic susceptibilities.
[34 ... Maksic, Z. B.; Eckert–Maksic, M.; Rupnik, K.
Croat Chem Acta 1984, 57, 1295.
35 ... Maksic, Z. B. J Mol Struct 1988, 170, 39.
36 ... Maksic, Z. B. In Molecules in Physics, Chemistry, and Biology;
Maruani, J., Ed.; Kluwer: Amsterdam, 1989, p. 49.]
Most recently, it is providing a novel means of partitioning space in a
crystal into molecules for visualization and other purposes.
[37 ... Spackman, M. A.; Byrom, P. G. Chem Phys Lett 1997, 267, 215.
38 ... McKinnon, J. J.; Mitchell, A. S.; Spackman, M. A.
Chem Eur J 1998, 4, 2136.
39 ... McKinnon, J. J.; Mitchell, A. S.; Spackman, M. A.
Chem Commun 1998, 2071.
xx ... “Molecular Surfaces from the Promolecule: A Comparison with
Hartree-Fock Ab Initio Electron Density Surfaces”
Mitchell, A. S.; Spackman, M. A. J. Comput. Chem. 2000,
21, 933-942.]
The use of high quality atomic wave functions provides an excellent description of the atomic densities, and our promolecule electron density surface is defined by an isosurface of the function ρ(r) = ∑A ∈ molecule ρA(r) where ρA(r) is the spherically averaged atomic electron density due to atom A, and the total electron density ρ(r) is simply the sum of the individual atomic electron densities, each located at the appropriate nucleus.
“Bonded and promolecule radii for molecules and crystals”
Gibbs, G. V.; Spackman, M. A.; Boisen, M. B. Am. Mineral. 1992, 77, 741.
A promolecule is defined to be a model of a molecule where the electron density distributions of each of its atoms have been spherically averaged and placed at their minimum energy positions (Hirshfeld and Rzotkiewicz, 1974).
“Chemical Properties from the Promolecule”
Spackman, M. A.; Maslen, E. N. J . Phys. Chem. 1986, 90, 2020-2027.
The term promolecule, originally used by Hirshfeld and Rzotkiewicz, [Hirshfeld, F. L.; Rzotkiewicz, S. Mol Phys 1974, 27, 1319.] refers to a reference electron density model prior to molecule formation. It is equivalent to the IAM model in electron scattering, [Bonham, R. A,; Fink, M. High Energy Electron Scattering; Van Nostrand-Reinhold: New York, 1974.] and the spherical atom approximation in X-ray crystallography. [(a) Hirshfeld, F. L. Isr. J. Chem. 1977, 16, 87-229. (b) Becker, P., Ed. Electron and Magnetization Densities in Molecules and Crystals; Plenum: New York, 1980. (c) Coppens, P., Hall, M. B., Eds. Electron Distributions and the Chemical Bond; Plenum: New York, 1982.]
In 1970 Politzer and Harris proposed a definition of the charges associated
with the atoms in a molecule in terms of the molecular electronic density:
“if the total space of the molecule could be partitioned into regions
belonging to the individual atoms, then the electronic charge associated with
a given atom could be determined by integrating the electronic density over the
region of space belonging to that atom”[1Politzer, Peter; Harris, Roger R.
J. Am. Chem.
Soc. 1970, 92, 6451-6454.]
| pi = ∫ Vi ρ(ri) d3ri | (1) |
where the integration is to be performed over the region of space Vi belonging to atom i. Based on this, the sum of all atom populations, pi, in the molecule provides the total electronic charge (i.e. the number of electrons) of the molecule.
| Natoms ∑ i=1 pi = ∫ V ρ(r) d3r | (2) |
where the integration is now performed over all the region of space thet contains the molecule.
Politzer and Harris used this definition to calculate the atomic charges
in three linear molecules, i.e. acetylene, lithium acetylide and
fluoroethyne.[1Politzer, Peter; Harris,
Roger R.
J. Am. Chem. Soc. 1970, 92,
6451-6454.] Here we review their method for educational purposes.
The components of the position vector r in eq (1) are the
cartesian coordinates x, y and z, and the volume element
dV is given by the product of the differentials of the
cartesian coordinates, dV = dx dy dz
= d3r.
The shape of linear molecules actually imposes the use of cylindrical
coordinates
| x = R cosφ, y = R sinφ, z = z | (3) |
where z is assumed to be the molecular axis. The volume element
dV changes by the Jacobian determinant of the coordinate
change,[L2PAMoC manual. Online resource:
“Methods of Numerical Integration”
“§ 1.5 - Transformation of coordinates”, equation
(1.32)] i.e.
dV = dx dy dz = det
| (4) |
Then, the volume integral (2) can be written as a three-dimensional integral in terms of the cylindrical coordinates R, φ, and z:
| ∫ V ρ(r) d3r = +∞ ∫ −∞ dz +∞ ∫ 0 R dR 2π ∫ 0 ρ(z,R,φ) dφ = +∞ ∫ −∞ g(z) dz | (5) |
where the radial probability density (also referred to as the radial
distribution), g(z), gives the probability of finding the
electron anywhere on the xy-plane perpendicular to the molecular axis at
z. In other words, it “is the density of electrons in this
plane”[2Brown, Richard E.; Shull,
Harrison
Int. J. Quantum Chem. 1968, 2,
663-685.] and can be designated “planar density”:[2Brown, Richard E.; Shull, Harrison
Int. J. Quantum Chem. 1968, 2, 663-685.]
| g(z) = +∞ ∫ 0 R dR 2π ∫ 0 ρ(z,R,φ) dφ = +∞ ∫ 0 R f(z,R) dR | (6) |
where the function f(z,R) represents the angular integral
| f(z,R) = 2π ∫ 0 ρ(z,R,φ) dφ | (7) |
The basic procedure[1Politzer, Peter;
Harris, Roger R.
J. Am. Chem. Soc. 1970, 92,
6451-6454.] consists in computing the “electron-count”
function for the linear molecule; the electron count is defined as[2Brown, Richard E.; Shull, Harrison
Int. J. Quantum Chem. 1968, 2, 663-685.]
| G(z) = z ∫ −∞ g(z) dz | (8) |
It simply denotes the number of electrons on the negative side of the xy-plane intersecting the z-axis at the point z.
As the first step, we need the rules for numerical quadratures over the cylindrical coordinates R, φ, and z. We can choose the most appropriate ones, among those described in the PAMoc manual page on “Methods of Numerical Integration”. For the angular integral (7) over the interval [0, 2π], we choose the closed extended trapezoidal rule
| f(z,R) = 2π ∫ 0 ρ(z,R,φ) dφ ≈ 2π nφ nφ ∑ i=1 ρ(z,R,φi) | (9) |
where φi = (i − 1) (2π/nφ), ∀ i = 1, 2, …, nφ. To solve the radial integral (6) we need a quadrature rule that spans the interval [0, +∞], like the generalized Gauss-Laguerre rule. However, the integrand R f(z,R) in eq (6) doesn't exactly correspond to the integrand of the quadrature formula, so let's rewrite it as follows
| R f(z,R) = R e−R e+R f(z,R) = R e−R F(z,R) | (10) |
where we have set F(z,R) = eR f(z,R). The last expression in eq (10) has the proper form required for the integrand of the generalized Gauss-Laguerre quadrature rule for α = 1, then we obtain a solution of the radial integral (6):
| g(z) = +∞ ∫ 0 R e−R F(z,R) dR ≈ nR ∑ i=1 wi F(z,Ri) = nR ∑ i=1 wi eRi f(z,Ri) | (11) |
where Ri are the roots of the generalized Laguerre polynomial of order nR and α = 1, with the associated weights wi. Finally, the integral (8) is estimated by evaluating g(z) at a number nz of points, zi, evenly spaced by a small interval h and then applying the closed extended trapezoidal rule
| G(znz) ≈ h nz ∑ i=1 g(zi) | (12) |
$contrl scftyp=rhf dfttyp=none runtyp=energy AIMPAC=.T. $end $system timlim=4 $end $guess guess=huckel $end $basis gbasis=N31 ngauss=6 ndfunc=1 $end $ELMOM IEMOM=3 IAMM=4 CUM=.TRUE. $END $ELFLDG IEFLD=2 $END $ELPOT IEPOT=1 $END $ELDENS IEDEN=1 $END $data CO at the experimental ground state geometry Cnv 4 C 6.0 0.0 0.0 0.0 O 8.0 0.0 0.0 1.128323 $end
The experimental bond length (rCO = 1.1283 Å
or 2.1322 bohr)[3(a) Tiemann, E.;
Arnst, H.; Stieda, W. U.; Törring, T.; Hoeft, J.
Chem. Phys. 1982 67, 133-138.
(b) Frenking,G.; Loschen, C.; Krapp, A.; Fau, S.; Strauss, S. H.
J. Comput. Chem. 2007, 28, 117-126.
(c) Demaison, J.; Császár, A. G.
J. Mol. Struct. 2012, 1023, 7-14.]
is used for the calculation.
The z axis is chosen to be identical with the molecular axis, and
z increases from left to right when the molecule is written CO, with
z = 0 corresponding to the carbon atom.
Thus the electron count, G(z), is the number of electrons to
the left of a plane passing through the molecular axis at the point
z.
Thanks to the option AIMPAC=.T. specified in the $CONTROL
group of the input, GAMESS provides an AIMPAC .wfn file that can be extracted
from the .dat file at the end of the computation.
(show the wfn file)
CO at the experimental ground state geometry
GAUSSIAN 7 MOL ORBITALS 56 PRIMITIVES 2 NUCLEI
C 1 (CENTRE 1) 0.00000000 0.00000000 0.00000000 CHARGE = 6.0
O 2 (CENTRE 2) 0.00000000 0.00000000 2.13222130 CHARGE = 8.0
CENTRE ASSIGNMENTS 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
CENTRE ASSIGNMENTS 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2
CENTRE ASSIGNMENTS 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
TYPE ASSIGNMENTS 1 1 1 1 1 1 1 1 1 2 2 2 3 3 3 4 4 4 1 2
TYPE ASSIGNMENTS 3 4 5 6 7 8 9 10 1 1 1 1 1 1 1 1 1 2 2 2
TYPE ASSIGNMENTS 3 3 3 4 4 4 1 2 3 4 5 6 7 8 9 10
EXPONENTS 3.0475249E+03 4.5736952E+02 1.0394868E+02 2.9210155E+01 9.2866630E+00
EXPONENTS 3.1639270E+00 7.8682723E+00 1.8812885E+00 5.4424926E-01 7.8682723E+00
EXPONENTS 1.8812885E+00 5.4424926E-01 7.8682723E+00 1.8812885E+00 5.4424926E-01
EXPONENTS 7.8682723E+00 1.8812885E+00 5.4424926E-01 1.6871448E-01 1.6871448E-01
EXPONENTS 1.6871448E-01 1.6871448E-01 8.0000000E-01 8.0000000E-01 8.0000000E-01
EXPONENTS 8.0000000E-01 8.0000000E-01 8.0000000E-01 5.4846717E+03 8.2523495E+02
EXPONENTS 1.8804696E+02 5.2964500E+01 1.6897570E+01 5.7996353E+00 1.5539616E+01
EXPONENTS 3.5999336E+00 1.0137618E+00 1.5539616E+01 3.5999336E+00 1.0137618E+00
EXPONENTS 1.5539616E+01 3.5999336E+00 1.0137618E+00 1.5539616E+01 3.5999336E+00
EXPONENTS 1.0137618E+00 2.7000582E-01 2.7000582E-01 2.7000582E-01 2.7000582E-01
EXPONENTS 8.0000000E-01 8.0000000E-01 8.0000000E-01 8.0000000E-01 8.0000000E-01
EXPONENTS 8.0000000E-01
MO 1 OCC NO = 2.00000000 ORB. ENERGY = -20.67514466
-2.15008108E-06 -3.96647976E-06 -6.40312820E-06 -8.33497036E-06 -7.11224531E-06
-2.45568739E-06 3.28313485E-05 1.51319385E-05 -4.24315352E-05 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
5.99401113E-04 4.59582755E-04 2.29364005E-04 1.73291995E-04 0.00000000E+00
0.00000000E+00 9.02410690E-05 -7.84628515E-05 -7.84628515E-05 9.76129351E-04
0.00000000E+00 0.00000000E+00 0.00000000E+00 -8.27295385E-01 -1.52266514E+00
-2.46395962E+00 -3.23894389E+00 -2.77802335E+00 -9.49853364E-01 1.29946094E-02
5.79816938E-03 -1.71220718E-02 0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 5.22448558E-03 4.02518449E-03
1.76727280E-03 -1.37722705E-03 0.00000000E+00 0.00000000E+00 1.13921873E-04
4.68071252E-03 4.68071252E-03 3.63599898E-03 0.00000000E+00 0.00000000E+00
0.00000000E+00
MO 2 OCC NO = 2.00000000 ORB. ENERGY = -11.36115332
-5.34178708E-01 -9.85455411E-01 -1.59083059E+00 -2.07078874E+00 -1.76700779E+00
-6.10105325E-01 1.01067841E-02 4.65820757E-03 -1.30621002E-02 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
-5.49233781E-03 -4.21117627E-03 -2.10167210E-03 3.38369935E-04 0.00000000E+00
0.00000000E+00 -1.12002255E-04 2.90821014E-03 2.90821014E-03 -3.44369354E-04
0.00000000E+00 0.00000000E+00 0.00000000E+00 5.85873559E-04 1.07832010E-03
1.74492547E-03 2.29375337E-03 1.96733894E-03 6.72666596E-04 3.05192252E-04
1.36176188E-04 -4.02130107E-04 0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 3.61903193E-04 2.78826900E-04
1.22420027E-04 9.83974379E-04 0.00000000E+00 0.00000000E+00 -8.93607081E-04
-2.20735035E-04 -2.20735035E-04 8.44110285E-04 0.00000000E+00 0.00000000E+00
0.00000000E+00
MO 3 OCC NO = 2.00000000 ORB. ENERGY = -1.51899106
-6.11553421E-02 -1.12819665E-01 -1.82125920E-01 -2.37073833E-01 -2.02295531E-01
-6.98477856E-02 -8.59553936E-02 -3.96167624E-02 1.11089537E-01 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
2.72313414E-01 2.08792654E-01 1.04202167E-01 7.99181089E-03 0.00000000E+00
0.00000000E+00 -2.24894768E-03 -2.41938378E-02 -2.41938378E-02 4.18113198E-02
0.00000000E+00 0.00000000E+00 0.00000000E+00 -1.67222693E-01 -3.07779023E-01
-4.98044557E-01 -6.54693511E-01 -5.61526820E-01 -1.91995556E-01 -2.76636071E-01
-1.23434476E-01 3.64503661E-01 0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 -5.02926007E-01 -3.87477376E-01
-1.70123439E-01 9.45822657E-02 0.00000000E+00 0.00000000E+00 -1.16987988E-02
-1.73116042E-03 -1.73116042E-03 2.32778399E-02 0.00000000E+00 0.00000000E+00
0.00000000E+00
MO 4 OCC NO = 2.00000000 ORB. ENERGY = -0.79655366
6.97146334E-02 1.28609886E-01 2.07616233E-01 2.70254647E-01 2.30608780E-01
7.96236698E-02 1.16065398E-01 5.34944358E-02 -1.50003982E-01 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
-1.56200838E-01 -1.19764895E-01 -5.97710765E-02 -3.41753678E-02 0.00000000E+00
0.00000000E+00 3.97388085E-03 1.52861647E-02 1.52861647E-02 -1.34816359E-02
0.00000000E+00 0.00000000E+00 0.00000000E+00 -8.93048769E-02 -1.64368647E-01
-2.65979497E-01 -3.49637494E-01 -2.99882047E-01 -1.02534765E-01 -1.59068295E-01
-7.09759635E-02 2.09592971E-01 0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 1.55934488E+00 1.20139117E+00
5.27475432E-01 1.06229058E-01 0.00000000E+00 0.00000000E+00 6.89979525E-02
1.05398325E-02 1.05398325E-02 -2.80807110E-02 0.00000000E+00 0.00000000E+00
0.00000000E+00
MO 5 OCC NO = 2.00000000 ORB. ENERGY = -0.63283386
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 -0.00000000E+00 -0.00000000E+00 0.00000000E+00 -3.67788275E-01
-2.81996721E-01 -1.40736128E-01 0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 -1.79922202E-02
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 -8.95996166E-02 0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 -0.00000000E+00
-0.00000000E+00 0.00000000E+00 -1.73228951E+00 -1.33463568E+00 -5.85976951E-01
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 -1.03132678E-01 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 7.96887774E-02
0.00000000E+00
MO 6 OCC NO = 2.00000000 ORB. ENERGY = -0.63283386
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 -0.00000000E+00 -0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 -3.67788275E-01 -2.81996721E-01 -1.40736128E-01
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
-1.79922202E-02 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 -8.95996166E-02 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 -0.00000000E+00
-0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
-1.73228951E+00 -1.33463568E+00 -5.85976951E-01 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 -1.03132678E-01 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
7.96887774E-02
MO 7 OCC NO = 2.00000000 ORB. ENERGY = -0.54768783
-7.61389046E-02 -1.40461412E-01 -2.26748271E-01 -2.95158875E-01 -2.51859603E-01
-8.69610684E-02 -1.11606749E-01 -5.14394487E-02 1.44241583E-01 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00 0.00000000E+00
-5.79124322E-01 -4.44035798E-01 -2.21604983E-01 1.13989145E-01 0.00000000E+00
0.00000000E+00 -2.45312310E-02 1.03408897E-02 1.03408897E-02 -4.23783989E-02
0.00000000E+00 0.00000000E+00 0.00000000E+00 1.14521056E-02 2.10779877E-02
3.41081629E-02 4.48361348E-02 3.84556923E-02 1.31486543E-02 2.24926308E-02
1.00361681E-02 -2.96369387E-02 0.00000000E+00 0.00000000E+00 0.00000000E+00
0.00000000E+00 0.00000000E+00 0.00000000E+00 8.02537359E-01 6.18311771E-01
2.71472171E-01 -2.72606041E-03 0.00000000E+00 0.00000000E+00 4.15442981E-02
4.28222412E-03 4.28222412E-03 -1.29610385E-02 0.00000000E+00 0.00000000E+00
0.00000000E+00
END DATA
RHF ENERGY = -112.7373122820 VIRIAL(-V/T) = 2.00312437
This wfn file can be opened in the interactive version of PAMOC to calculate the electron count function. The plot of G(z) vs. z is shown in Figure 1.
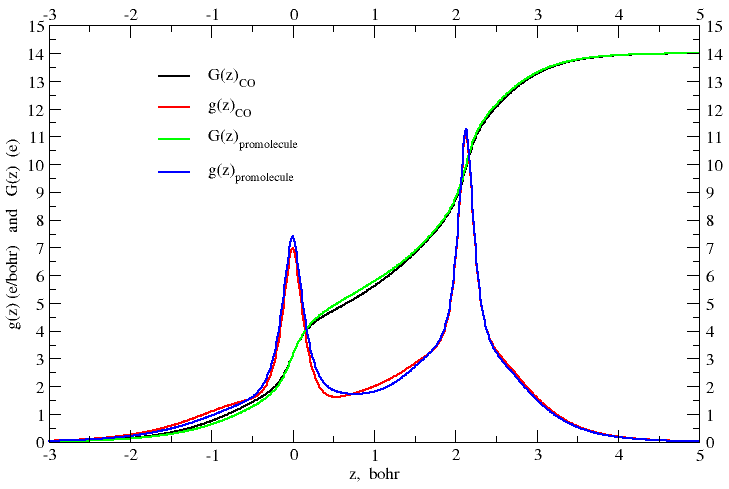
At this point, “it is necessary […] to decide upon a
reasonable and well-defined criterion in terms of which to partition
the space of the molecule. The criterion which is being proposed is as
follows. The atomic regions will be defined such that in the limiting
case of no interactions between the atoms, the electronic charge associated
with each one would be the same as for the free atom. This limiting case
can be represented by superposing free atom electronic densities, the atoms
being placed at the same relative positions as in the molecule.”[1Politzer, Peter; Harris, Roger R.
J.
Am. Chem. Soc. 1970, 92, 6451-6454.]
In the case of acetylene, lithium acetylide and fluoroethyne,
“the regions belonging to the individual atoms were determined
[…] in terms of the electron-count function for the superposed atoms.
The boundaries of the regions were established by means of hypothetical
planes which perpendicularly intersect the z axis at those points
for which G(z)promol = 1, 7, and 13.
These points on the z axis then define the regions belonging to
the atoms in the molecule. The number of electrons associated with each
atom could subsequently be obtained from the molecular electron-count
function; since the number of protons is known for each atom, the net atomic
charge follows immediately.”[1Politzer,
Peter; Harris, Roger R.
J. Am. Chem. Soc. 1970, 92,
6451-6454.]
This recipe is applied to CO in Figure 2, which shows an enlarged detail
of Figure 1. The electron count function of the promolecule,
G(z)promol, equals the number
of protons in the carbon nucleus (ZC = 6) when the
z-coordinate has the value zboundary = 1.1212 bohr.
The line perpendicular to the z-axis at zboundary
intersects the electron count function of CO at
G(zboundary)CO = 5.860 electrons, so
that the carbon is found to be positively charged by q(C) =
6 e − 5.860 e = + 0.140 e. This result is consistent with the
calculated Mulliken and Lowdin atomic populations:
TOTAL MULLIKEN AND LOWDIN ATOMIC POPULATIONS
ATOM MULL.POP. CHARGE LOW.POP. CHARGE
1 C 5.715758 0.284242 5.916101 0.083899
2 O 8.284242 -0.284242 8.083899 -0.083899
It is worth noting that the limiting case of non-interacting atoms used by Politzer and Harris as a reference is represented by the so-called promolecule density,[N1The promolecule.] even if the two authors have not made explicit use of this definition. In addition, the use of planes perpendicular to the internuclear axis to identify the boundaries of the atomic regions is an example of partitioning of the electron density in the real three-dimensional space into two unbounded Voronoi atomic cells.[N2Voronoi cell.] Again, the two authors do not give any explicit definition of their method of electron density partitioning, which however can be considered an extension of Voronoi's partitioning, since the boundary planes can be displaced from the bond midpoint (where, by definition, are located the faces of a Voronoi polyhedron).[N2Voronoi cell.]
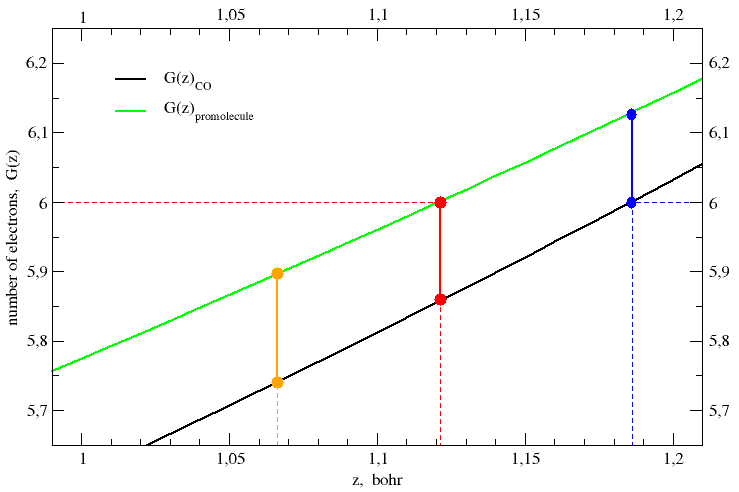
J. Am. Chem. Soc. 1970, 92, 6451-6454.] The black and green curves represent the electron-count function for the CO molecule and its promolecule, respectively. The red ball on the green curve is chosen in such a way its ordinate (i.e. the number of electrons on carbon) equals the number of protons in the carbon nucleus, ZC = 6. Its abscissa gives the position of the plane that separates the carbon atom from the oxygen atom, both in the promolecule and in the CO molecule. Of course, the ordinate of the red ball on the black curve gives the total number of electrons on the carbon in the CO molecule. The difference of the ordinates of the two red balls gives the partial charge or net atomic charge of carbon in the CO molecule. Politzer's rule is all here.
On the other hand, if you move a vertical line like a cursor along the internuclear axis, you identify two points that give the electron population of carbon at each z-value both in the CO molecule and in its promolecule.
Ultimately, the Politzer and Harris method consists of three steps:
- find the boundary plane, by determining the z-value where the electron count function of the promolecule has the same value of the free atom, i.e. G(z)promol = ZC;
- use the zboundary value thus found to evaluate G(zboundary)CO, i.e. the number of electrons belonging to the carbon atom;
- estimate the partial atomic charge on carbon by the difference:
q(C) = G(zboundary)promol − G(zboundary)CO = ZC − G(zboundary)CO = + 0.140 e (13)
The definition of atomic charge proposed by Politzer and Harris
“admittedly contains an element of arbitrariness in that the atomic
regions could be defined in terms of other criteria than the requirement
that the atoms have zero charges in the limit of no interaction.”.[1Politzer, Peter; Harris, Roger R.
J. Am. Chem. Soc. 1970, 92, 6451-6454.]
Indeed, by removing this constraint, imposed by the first step in the
above scheme, and allowing to choose for zboundary any
appropriate value between the two bonded atoms, we can obtain partial charges
that better describe the properties of the molecule. As a consequence of this
choice, the two differences in eq (13) turn out to provide two different
models, so that in general they'll give different results.
In particular, the first difference defines the partial atomic charge
due to the deformation density, that is the density change
when going from the superposition of atomic densities to the final molecular
density.
| qVDD = −[ G(zboundary)mol − G(zboundary)promol ] = −[ zboundary ∫ −∞ g(z)mol dz − zboundary ∫ −∞ g(z)promol dz ] = − zboundary ∫ −∞ g(z)DD dz | (14) |
where g(z)DD = g(z)mol − g(z)promol is the deformation density. Essentially, eq (14) is an example of application of the VDD method.
The last difference in eq (13) is the usual definition of partial atomic charge
| zboundary, bohr | G(zboundary)promol, e | G(zboundary)mol, e | qVDD, e | qVP, e |
|---|---|---|---|---|
| 1.0661 (= ½rCO) | 5.895 | 5.740 | 0.155 | 0.260 |
| 1.1212 (⇒ Gpromol = 6) | 6.000 | 5.857 | 0.143 | 0.143 |
| 1.1258 | 6.009 | 5.867 | 0.142 | 0.133 |
| 1.1411 | 6.039 | 5.900 | 0.139 | 0.100 |
| 1.1863 (⇒ Gmol = 6) | 6.129 | 6.000 | 0.129 | 0.000 |
| 1.2422 | 6.245 | 6.129 | 0.116 | −0.129 |
Although in general the choice of the midpoint of the internuclear axis
would be rather unrealistic,[1Politzer, Peter; Harris, Roger R.
J. Am. Chem.
Soc. 1970, 92, 6451-6454.] and indeed
in the case of CO the criterion proposed by Politzer and Harris finds a
boundary plane placed 0.0551 bohr beyond the bond midpoint
(½ rCO = 1.0661 bohr), and actually this is not
even enough, because it would be necessary to move the boundary plane at
z > bohr to find a partial negative charge on the carbon, as it was
observed experimentally.[4Muenter, J. S.
J. Mol. Spectr. 1975, 55, 490-491.]
On the other hand,
placing the boundary plane at z = ½ rCO.
References
- “Properties of Atoms in Molecules. I. A Proposed Definition
of the Charge on an Atom in a Molecule”
Politzer, Peter; Harris, Roger R. J. Am. Chem. Soc. 1970, 92, 6451-6454. - “A Configuration Interaction Study of the Four Lowest
1Σ+ States of the LiH Molecule”
Brown, Richard E.; Shull, Harrison Int. J. Quantum Chem. 1968, 2, 663-685. - (a) “Observed adiabatic corrections to the
Born-Oppenheimer approximation for diatomic molecules with ten
valence electrons”
Tiemann, E.; Arnst, H.; Stieda, W. U.; Törring, T.; Hoeft, J. Chem. Phys. 1982 67, 133-138.
(b) “Electronic Structure of CO − An Exercise in Modern Chemical Bonding Theory”
Frenking,G.; Loschen, C.; Krapp, A.; Fau, S.; Strauss, S. H. J. Comput. Chem. 2007, 28, 117-126.
(c) “Equilibrium CO bond lengths”
Demaison, J.; Császár, A. G. J. Mol. Struct. 2012, 1023, 7-14. - “Electric Dipole Moment of Carbon Monoxide”
Muenter, J. S. J. Mol. Spectr. 1975, 55, 490-491. - (a) “The Carbon-Lithium Electron Pair Bond in
(CH3Li)n (n = 1, 2, 4)”
Bickelhaupt, F. M.; van Eikema Hommes, N. J. R.; Fonseca Guerra, C.; Baerends, E. J. Organometallics 1996, 15, 2923-2931.
(b) “Voronoi Deformation Density (VDD) Charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD Methods for Charge Analysis”
Fonseca Guerra, C.; Handgraaf, J.-W.; Baerends, E. J.; Bickelhaupt, F. M. J. Comput. Chem. 2004, 25, 189-210.
(b) “How amino and nitro substituents direct electrophilic aromatic substitution in benzene: an explanation with Kohn-Sham molecular orbital theory and Voronoi deformation density analysis”
Stasyuk, O. A.; Szatylowicz, H.; Krygowskib, T. M.; Fonseca Guerra, C. Phys. Chem. Chem. Phys. 2016, 18, 11624-11633. - “Atomic charges from modified Voronoi polyhedra”
Rousseau, B.; Peeters, A.; Van Alsenoy, C. Journal of Molecular Structure (Theochem) 2001, 538, 235-238.
Notes
- Promolecule. The promolecule is an ideal reference system made up by non-interacting atoms placed at the same positions they occupy in the molecule. Then the promolecule density is a superposition of the free-atom electron densities (usually spherically averaged) centred at the positions of the atoms in the molecule.
- Voronoi Polyhedra. The Voronoi polyhedra were first
defined by mathematicians [a,b] and are variously known as Dirichlet [a]
regions, Voronoi [b] polyhedra, Wigner-Seitz [c] cells, or domains [d].
[a] Dirichlet, G. L. “Über die Reduction der positiven quadratischen Formen mit drei unbestimmten ganzen Zahlen.” Journal für die reine und angewandte Mathematik 1850, 40, 209-227.
[b] Voronoi, G. F. “Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs.” Journal für die reine und angewandte Mathematik 1908, 134, 198-287.
[c] Wigner, E. P.; Seitz, F. “On the Constitution of Metallic Sodium.” Phys. Rev. 1933, 43, 804.
[d] Frank, F. C.; Kasper, J. S. “Complex alloy structures regarded as sphere packings. I. Definitions and basic principles.” Acta Crystallogr. 1958, 11, 184-190.
Voronoi polyhedra are intersections of half-spaces; they are convex but not necessarily bounded. A half-space is either of the two parts into which a plane divides the three-dimensional Euclidean space. That is, the points that are not incident to the plane are partitioned into two convex sets (i.e., half-spaces), such that any subspace connecting a point in one set to a point in the other must intersect the plane.
Voronoi polyhedra can be constructed in the following manner. Consider a set of points P1, P2, …, Pn in the three-dimensional Euclidean space ℝ. Consider the line interconnecting the point Pi and one of its neighbors Pj. Construct a plane hij perpendicular to this line at its midpoint zij. Repeating this process for all points Pj yields a set of planes that define a polyhedron around point Pi. The set of Voronoi polyhedra corresponding to a given configuration of centers is called the Voronoi diagram.
So, the Voronoi polyhedron Vi around a given center Pi, is the set of points in ℝ closer to Pi than to any Pj: more formally,
where d denotes distance. We call Hij the half-space generated by hij that consists of the subset of ℝ on the same side of hij as Pi; that is,Vi = {x ∈ ℝ : d(x, Pi) ≤ d(x, Pj), j = 1, 2 , …, n}, (N2.1)
Vi is bounded by faces, with each face fij belonging to a distinct plane hij. Each face is characterized by listing its vertices and edges in cyclic order.Vi = ⋂ j Hij. (N2.2)
[Source of this note is paper “Construction of Voronoi Polyhedra” by Witold Brostow and Jean-Pierre Dussault on the Journal of Computational Physics, 1978, 29, 81-92.]
Links
-
 Dr. Peter Politzer's page (http://www.clevetheocomp.org/peter.html)
Dr. Peter Politzer's page (http://www.clevetheocomp.org/peter.html)
and publications (https://www.researchgate.net/scientific-contributions/38975283_Peter_Politzer/publications).
Accessed 12 Jan 2018. - PAMoC manual. Online resource: “Methods of Numerical
Integration”
“§ 1.5 - Transformation of coordinates”, equation (1.32). - “GAMESS: General Atomic and Molecular Electronic Structure
System”. Online resource: http://www.msg.ameslab.gov/gamess/.
Accessed 1 Dec 2017.